Question

【題目】如圖①，有一個等腰直角三角板垂直于平面，有一條長為7的細線，其兩端分別位于處，現用鉛筆拉緊細線，在平面上移動.

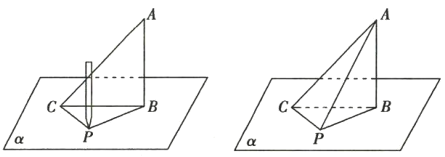
圖① 圖②

（1）圖②中的的長為多少時，平面？并給出證明.

（2）在（1）的情形下，求三棱錐的高.

Answer 1

【答案】（1）當時，平面，證明見解析；（2）.

【解析】

（1）若使得平面，則需三角形為直角三角形且，當時，根據線面線面垂直的判定定理，證明即可.

（2）方法一，過點作于點，由（1）可知，，則平面，即為三棱錐的高，在中計算，再根據，求解即可. 方法二，設三棱錐的高為，根據，求解即可.

（1）當時，平面.證明如下：

若，則

因為，所以

所以三角形為直角三角形，且.

又因為平面平面，平面平面，平面

所以平面.

因為平面

所以.

又因為平面，平面，.

所以平面.

（2）方法一 如圖，過點作于點.

由（1）知平面，平面

所以.

又平面，平面，，

所以平面，即為三棱錐的高.

由于平面，所以，

由，得.即三棱錐的高為.

方法二 由（1），知平面，平面

所以.

又，

所以，即.

設三棱錐的高為，則.

又，

且，所以，即.

所以三棱錐的高為.