
【題目】已知實數![]() 滿足
滿足![]() ,且
,且![]() .證明:存在整數
.證明:存在整數![]() ,使得
,使得![]() .
.
【答案】證明見解析
【解析】
記![]() .
.
構造下列51個數:![]() ,
,
![]() ,
,
![]() .
.
下面證明![]() 中至少有一個在區間
中至少有一個在區間![]() 內.
內.
由上述符號的含義,
知![]()
![]() ,
,
且![]() .
.
所以![]() .
.
(1)若![]() ,則由
,則由![]() ,得
,得![]() .
.
因此![]()
![]() .
.
(2)若![]() ,假設
,假設![]() 都不在區間
都不在區間![]() 內,
內,
則由![]() ,知
,知![]() .
.
結合假設,得![]() .
.
又由![]() ,知
,知![]() .
.
所以![]() 中存在比
中存在比![]() 小的數,也存在比
小的數,也存在比![]() 大的數.
大的數.
又![]() ,且
,且![]() 都不在區間
都不在區間![]() 內.
內.
因此,存在j∈{1,2,……,50},使得![]() .
.
此時,![]() .
.
另一方面,![]() ,兩者矛盾.
,兩者矛盾.
所以![]() 中至少有一個在區間
中至少有一個在區間![]() 內.
內.
由(1)(2)知,![]() 中至少有一個在區間
中至少有一個在區間![]() 內.
內.
由![]() 的定義知,結論成立
的定義知,結論成立
解法二:首先用數學歸納法證明
對于任意正整數n,若實數![]() 滿足
滿足![]() ,
,
則存在![]() 的一個排列
的一個排列![]() ,
,
使得![]() .
.
證明如下:(1)當n=1時,結論顯然成立
(2)假設當n=k時,結論成立,
則當n=k+1時,由歸納假設知,存在![]() 的一個排列
的一個排列![]() ,
,
使得![]() .
.
記![]() ,
,![]() ,
,
則![]() .從而當
.從而當![]() 時:
時:
![]()
![]() ;
;
當![]() 時:
時:
![]()
![]() .
.
即當n=k+1時,結論也成立.
由(1)(2)知,對于任意正整數n,結論都成立.
回到本題,利用上述結論容易知道存在![]() 的一個排列
的一個排列![]() 滿足
滿足![]() ,
,![]() ,
,
且![]() .
.
又![]() ,
,
所以![]() 或
或![]() .
.
因此結論成立.


科目:高中數學 來源: 題型:
【題目】下列結論中正確的個數是( )
①在![]() 中,“
中,“![]() ”是“
”是“![]() ”的必要不充分條件;
”的必要不充分條件;
②若![]() ,
,![]() 的最小值為2;
的最小值為2;
③夾在圓柱的兩個平行截面間的幾何體是圓柱;
④數列![]() 的通項公式為
的通項公式為![]() ,則數列的前
,則數列的前![]() 項和
項和![]() .( )
.( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】線段AB為圓![]() 的一條直徑,其端點A,B在拋物線
的一條直徑,其端點A,B在拋物線![]() 上,且A,B兩點到拋物線C焦點的距離之和為11.
上,且A,B兩點到拋物線C焦點的距離之和為11.
(1)求拋物線C的方程及直徑AB所在的直線方程;
(2)過M點的直線l交拋物線C于P,Q兩點,拋物線C在P,Q處的切線相交于N點,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為利于分層教學,某學校根據學生的情況分成了![]() ,
,![]() ,
,![]() 三類,經過一段時間的學習后在三類學生中分別隨機抽取了1個學生的5次考試成績,其統計表如下:
三類,經過一段時間的學習后在三類學生中分別隨機抽取了1個學生的5次考試成績,其統計表如下:
![]() 類
類
第 | 1 | 2 | 3 | 4 | 5 |
分數 | 145 | 83 | 95 | 72 | 110 |
![]() ,
,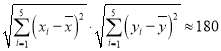 ;
;
![]() 類
類
第 | 1 | 2 | 3 | 4 | 5 |
分數 | 85 | 93 | 90 | 76 | 101 |
![]() ,
,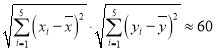 ;
;
![]() 類
類
第 | 1 | 2 | 3 | 4 | 5 |
分數 | 85 | 92 | 101 | 100 | 112 |
![]() ,
,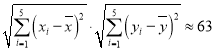 ;
;
(1)經計算已知![]() ,
,![]() 的相關系數分別為
的相關系數分別為![]() ,
,![]() ,請計算出
,請計算出![]() 學生的
學生的![]() 的相關系數,并通過數據的分析回答抽到的哪類學生學習成績最穩定;(結果保留三位有效數字,
的相關系數,并通過數據的分析回答抽到的哪類學生學習成績最穩定;(結果保留三位有效數字,![]() 越大認為成績越穩定);
越大認為成績越穩定);
(2)利用(1)中成績最穩定的學生的樣本數據,已知線性回歸方程為![]() ,利用線性回歸方程預測該生第九次的成績.
,利用線性回歸方程預測該生第九次的成績.
參考公式:(1)樣本![]() 的相關系數
的相關系數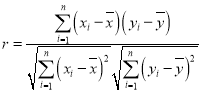 ;
;
(2)對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸方程
,其回歸方程![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為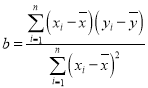 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖兩個同心球,球心均為點![]() ,其中大球與小球的表面積之比為3:1,線段
,其中大球與小球的表面積之比為3:1,線段![]() 與
與![]() 是夾在兩個球體之間的內弦,其中
是夾在兩個球體之間的內弦,其中![]() 兩點在小球上,
兩點在小球上,![]() 兩點在大球上,兩內弦均不穿過小球內部.當四面體
兩點在大球上,兩內弦均不穿過小球內部.當四面體![]() 的體積達到最大值時,此時異面直線
的體積達到最大值時,此時異面直線![]() 與
與![]() 的夾角為
的夾角為![]() ,則
,則![]() ( )
( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,底面ABCD是邊長為2的菱形,點E,F分別為棱DC,BC的中點,點G是棱SC靠近點C的四等分點.
,底面ABCD是邊長為2的菱形,點E,F分別為棱DC,BC的中點,點G是棱SC靠近點C的四等分點.
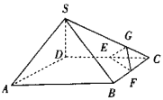
求證:(1)直線![]() 平面EFG;
平面EFG;
(2)直線![]() 平面SDB.
平面SDB.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com