
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,其短軸的兩個端點與長軸的一個端點構成的三角形的面積為
,其短軸的兩個端點與長軸的一個端點構成的三角形的面積為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() 與圓
與圓![]() 相切,并與橢圓
相切,并與橢圓![]() 交于不同的兩點
交于不同的兩點![]() 和
和![]() ,若
,若![]() 為坐標原點),求線段
為坐標原點),求線段![]() 長度的取值范圍.
長度的取值范圍.
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的短軸長為
的短軸長為![]() ,離心率為
,離心率為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)設橢圓![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
,![]() 左,右頂點分別為
左,右頂點分別為![]() ,
,![]() ,點
,點![]() ,
,![]() ,為橢圓
,為橢圓![]() 上位于
上位于![]() 軸上方的兩點,且
軸上方的兩點,且![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,記直線
,記直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某海濕地如圖所示,A、B和C、D分別是以點O為中心在東西方向和南北方向設置的四個觀測點,它們到點O的距離均為![]() 公里,實線PQST是一條觀光長廊,其中,PQ段上的任意一點到觀測點C的距離比到觀測點D的距離都多8公里,QS段上的任意一點到中心點O的距離都相等,ST段上的任意一點到觀測點A的距離比到觀測點B的距離都多8公里,以O為原點,AB所在直線為x軸建立平面直角坐標系xOy.
公里,實線PQST是一條觀光長廊,其中,PQ段上的任意一點到觀測點C的距離比到觀測點D的距離都多8公里,QS段上的任意一點到中心點O的距離都相等,ST段上的任意一點到觀測點A的距離比到觀測點B的距離都多8公里,以O為原點,AB所在直線為x軸建立平面直角坐標系xOy.
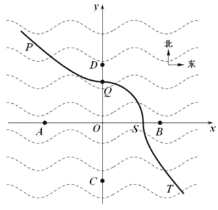
(1)求觀光長廊PQST所在的曲線的方程;
(2)在觀光長廊的PQ段上,需建一服務站M,使其到觀測點A的距離最近,問如何設置服務站M的位置?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司推出一新款手機,因其功能強大,外觀新潮,一上市便受到消費者爭相搶購,銷量呈上升趨勢.散點圖是該款手機上市后前6周的銷售數據.
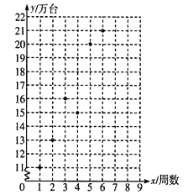
(Ⅰ)根據散點圖,用最小二乘法求![]() 關于
關于![]() 的線性回歸方程,并預測該款手機第8周的銷量;
的線性回歸方程,并預測該款手機第8周的銷量;
(Ⅱ)為了分析市場趨勢,該公司市場部從前6周的銷售數據中隨機抽取2周的數據,求抽到的這2周的銷量均在20萬臺以下的概率.
參考公式:回歸直線方程![]() ,其中:
,其中: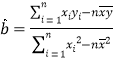 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,五邊形ABSCD中,四邊形ABCD為矩形,AB=1,△BSC為邊長為2的正三角形,將△BSC沿BC折起,使得側面SAD垂直于平面ABCD,E、F分別為SA、DC的中點.
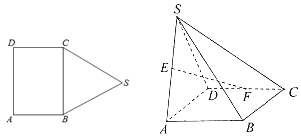
(1)求證:EF∥面SBC;
(2)求四棱錐S﹣ABCD的側面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一塊長方形區域![]() ,
,![]() ,
,![]() ,在邊
,在邊![]() 的中點
的中點![]() 處有一個可轉動的探照燈,其照射角
處有一個可轉動的探照燈,其照射角![]() 始終為
始終為![]() ,設
,設![]() ,探照燈照射在長方形
,探照燈照射在長方形![]() 內部區域的面積為
內部區域的面積為![]() .
.
(1)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)當![]() 時,求
時,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sinπx,g(x)=x2﹣x+2,則( )
A. 曲線y=f(x)+g(x)不是軸對稱圖形
B. 曲線y=f(x)﹣g(x)是中心對稱圖形
C. 函數y=f(x)g(x)是周期函數
D. 函數![]() 最大值為
最大值為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于![]() 的不等式
的不等式![]() 有且僅有兩個正整數解(其中e=2.71828… 為自然對數的底數),則實數
有且僅有兩個正整數解(其中e=2.71828… 為自然對數的底數),則實數![]() 的取值范圍是( )
的取值范圍是( )
A. (![]() ,
,![]() ] B. (
] B. (![]() ,
,![]() ] C. [
] C. [![]() ,
,![]() ) D. [
) D. [![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在底面是正三角形、側棱垂直于底面的三棱柱ABC﹣A1B1C1中,底面邊長為a,側棱長為2a,點M是A1B1的中點.
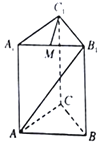
(1)證明:MC1⊥AB1.
(2)求直線AC1與側面BB1C1C所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com