
【題目】【2017福建三明5月質(zhì)檢】已知函數(shù)![]() ,
,![]() .
.
(Ⅰ)當(dāng)![]() 時,求證:過點
時,求證:過點![]() 有三條直線與曲線
有三條直線與曲線![]() 相切;
相切;
(Ⅱ)當(dāng)![]() 時,
時,![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(I)詳見解析;(II)![]() .
.
【解析】
解法一:(Ⅰ)當(dāng)![]() 時,
時,![]() ,
,
![]()
![]()
設(shè)直線與曲線![]() 相切,其切點為
相切,其切點為![]() ,
,
則曲線![]() 在點
在點![]() 處的切線方程為:
處的切線方程為:![]() ,
,
因為切線過點![]() ,所以
,所以![]() ,
,
即![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,
,
設(shè)![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() 在三個區(qū)間
在三個區(qū)間![]() 上至少各有一個根
上至少各有一個根
又因為一元三次方程至多有三個根,所以方程![]() 恰有三個根,
恰有三個根,
故過點![]() 有三條直線與曲線
有三條直線與曲線![]() 相切.
相切.
(Ⅱ)∵當(dāng)![]() 時,
時,![]() ,即當(dāng)
,即當(dāng)![]() 時,
時,![]()
∴當(dāng)![]() 時,
時,![]() ,
,
設(shè)![]() ,則
,則![]() ,
,
設(shè)![]() ,則
,則![]() .
.
(1)當(dāng)![]() 時,∵
時,∵![]() ,∴
,∴![]() ,從而
,從而![]() (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng)![]() 時,等號成立)
時,等號成立)
∴![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
又∵![]() ,∴當(dāng)
,∴當(dāng)![]() 時,
時,![]() ,從而當(dāng)
,從而當(dāng)![]() 時,
時,![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞減,又∵
上單調(diào)遞減,又∵![]() ,
,
從而當(dāng)![]() 時,
時,![]() ,即
,即![]()
于是當(dāng)![]() 時,
時,![]() .
.
(2)當(dāng)![]() 時,令
時,令![]() ,得
,得![]() ,∴
,∴![]() ,
,
故當(dāng)![]() 時,
時,![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
又∵![]() ,∴當(dāng)
,∴當(dāng)![]() 時,
時,![]() ,
,
從而當(dāng)![]() 時,
時,![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞增,又∵
上單調(diào)遞增,又∵![]() ,
,
從而當(dāng)![]() 時,
時,![]() ,即
,即![]()
于是當(dāng)![]() 時,
時,![]() ,
,
綜合得![]() 的取值范圍為
的取值范圍為![]() .
.
解法二:(Ⅰ)當(dāng)![]() 時,
時,![]() ,
,
![]()
![]() ,
,
設(shè)直線與曲線![]() 相切,其切點為
相切,其切點為![]() ,
,
則曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,
,
因為切線過點![]() ,所以
,所以![]() ,
,
即![]()
![]() ,
,
∵![]() ,∴
,∴![]()
設(shè)![]() ,則
,則![]() ,令
,令![]() 得
得![]()
當(dāng)![]() 變化時,
變化時,![]() ,
,![]() 變化情況如下表:
變化情況如下表:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| ↗ | 極大值
| ↘ | 極小值 | ↗ |
∴![]() 恰有三個根,
恰有三個根,
故過點![]() 有三條直線與曲線
有三條直線與曲線![]() 相切.
相切.
(Ⅱ)同解法一.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知f(x)= ![]() ,(a>0,且a≠1).
,(a>0,且a≠1).
(1)求f(x)的定義域.
(2)證明f(x)為奇函數(shù).
(3)求使f(x)>0成立的x的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若橢圓的對稱軸為坐標(biāo)軸,長軸長與短軸長的和為18,焦距為6,則橢圓的方程為( )
A.![]()
B.![]()
C.![]() 或
或 ![]()
D.以上都不對
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】【2017北京西城區(qū)5月模擬】某大學(xué)為調(diào)研學(xué)生在![]() ,
,![]() 兩家餐廳用餐的滿意度,從在
兩家餐廳用餐的滿意度,從在![]() ,
,![]() 兩家餐廳都用過餐的學(xué)生中隨機(jī)抽取了100人,每人分別對這兩家餐廳進(jìn)行評分,滿分均為60分.
兩家餐廳都用過餐的學(xué)生中隨機(jī)抽取了100人,每人分別對這兩家餐廳進(jìn)行評分,滿分均為60分.
整理評分?jǐn)?shù)據(jù),將分?jǐn)?shù)以10為組距分成6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到
,得到![]() 餐廳分?jǐn)?shù)的頻率分布直方圖,和
餐廳分?jǐn)?shù)的頻率分布直方圖,和![]() 餐廳分?jǐn)?shù)的頻數(shù)分布表:
餐廳分?jǐn)?shù)的頻數(shù)分布表:
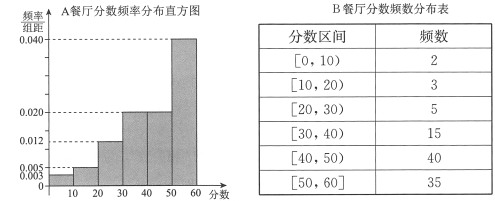
定義學(xué)生對餐廳評價的“滿意度指數(shù)”如下:
分?jǐn)?shù) |
|
|
|
滿意度指數(shù) |
|
|
|
(Ⅰ)在抽樣的100人中,求對![]() 餐廳評價“滿意度指數(shù)”為0的人數(shù);
餐廳評價“滿意度指數(shù)”為0的人數(shù);
(Ⅱ)從該校在![]() ,
,![]() 兩家餐廳都用過餐的學(xué)生中隨機(jī)抽取1人進(jìn)行調(diào)查,試估計其對
兩家餐廳都用過餐的學(xué)生中隨機(jī)抽取1人進(jìn)行調(diào)查,試估計其對![]() 餐廳評價的“滿意度指數(shù)”比對
餐廳評價的“滿意度指數(shù)”比對![]() 餐廳評價的“滿意度指數(shù)”高的概率;
餐廳評價的“滿意度指數(shù)”高的概率;
(Ⅲ)如果從![]() ,
,![]() 兩家餐廳中選擇一家用餐,你會選擇哪一家?說明理由.
兩家餐廳中選擇一家用餐,你會選擇哪一家?說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,程序框圖的輸出結(jié)果為﹣18,那么判斷框①表示的“條件”應(yīng)該是( ) 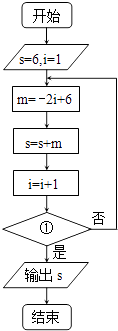
A.i>10?
B.i>9?
C.i>8?
D.i>7?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)直線l1 , l2分別是函數(shù)f(x)= ![]() 圖象上點P1 , P2處的切線,l1與l2垂直相交于點P,且l1 , l2分別與y軸相交于點A,B,則△PAB的面積的取值范圍是( )
圖象上點P1 , P2處的切線,l1與l2垂直相交于點P,且l1 , l2分別與y軸相交于點A,B,則△PAB的面積的取值范圍是( )
A.(0,1)
B.(0,2)
C.(0,+∞)
D.(1,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點A,B,C,D是直角坐標(biāo)系中不同的四點,若 ![]() =λ
=λ ![]() (λ∈R),
(λ∈R), ![]() =μ
=μ ![]() (μ∈R),且
(μ∈R),且 ![]() =2,則下列說法正確的是( )
=2,則下列說法正確的是( )
A.C可能是線段AB的中點
B.D可能是線段AB的中點
C.C,D可能同時在線段AB上
D.C,D不可能同時在線段AB的延長線上
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系xOy中,點P到兩點(0,﹣![]() ),(0,
),(0,![]() )的距離之和等于4,設(shè)點P的軌跡為C,直線y=kx+1與C交于A,B兩點.
)的距離之和等于4,設(shè)點P的軌跡為C,直線y=kx+1與C交于A,B兩點.
(1)寫出C的方程;
(2)若![]() ⊥
⊥![]() , 求k的值.
, 求k的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2012年“雙節(jié)”期間,高速公路車輛較多.某調(diào)查公司在一服務(wù)區(qū)從七座以下小型汽車中按進(jìn)服務(wù)區(qū)的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進(jìn)行詢問調(diào)查,將他們在某段高速公路的車速(km/t)分成六段:(60,65),[65,70),[70,75),[80,85),[85,90)后得到如圖的頻率分布直方圖.
(1)某調(diào)查公司在采樣中,用到的是什么抽樣方法?
(2)求這40輛小型車輛車速的眾數(shù)和中位數(shù)的估計值.
(3)若從車速在[60,70)的車輛中任抽取2輛,求車速在[65,70)的車輛至少有一輛的概率.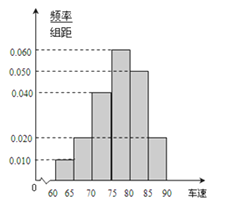
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com