【題目】已知數列
滿足
，
．
（1）求
；
（2）若
，證明：數列
中的任意三項不可能構成等差數列．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】某企業生產甲、乙兩種產品，銷售利潤分別為2千元/件、1千元/件.甲、乙兩種產品都需要在
兩種設備上加工，生產一件甲產品需用
設備2小時， 
設備6小時；生產一件乙產品需用
設備3小時， 
設備1小時. 
兩種設備每月可使用時間數分別為480小時、960小時，若生產的產品都能及時售出，則該企業每月利潤的最大值為（ ）
A. 320千元 B. 360千元 C. 400千元 D. 440千元
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某啤酒廠要將一批鮮啤酒用汽車從所在城市甲運至城市乙，已知從城市甲到城市乙只有兩條公路，運費由廠家承擔．若廠家恰能在約定日期（×月×日）將啤酒送到，則城市乙的銷售商一次性支付給廠家40萬元；若在約定日期前送到，每提前一天銷售商將多支付給廠家2萬；若在約定日期后送到，每遲到一天銷售商將少支付給廠家2萬元．為保證啤酒新鮮度，汽車只能在約定日期的前兩天出發，且只能選擇其中的一條公路運送．已知下表內的信息：
汽車行駛路線 | 在不堵車的情況下到達城市乙所需時間（天） | 在堵車的情況下到達城市乙所需時間（天） | 堵車的概率 | 運費（萬元） |
公路1 | 1 | 4 |
| 2 |
公路2 | 2 | 3 |
| 1 |
（1）記汽車選擇公路1運送啤酒時廠家獲得的毛收入為X（單位：萬元），求X的分布列和EX；
（2）若
，
，選擇哪條公路運送啤酒廠家獲得的毛收人更多？
（注：毛收入=銷售商支付給廠家的費用-運費）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，已知橢圓C:
(
>
>0)的右焦點為F(1，0)，且過點(1，
)，過點F且不與
軸重合的直線
與橢圓C交于A，B兩點，點P在橢圓上，且滿足
.
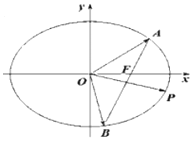
(1)求橢圓C的標準方程；
(2)若
，求直線AB的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左頂點為
，左、右焦點分別為
，離心率為
，
是橢圓上的一個動點（不與左、右頂點重合），且
的周長為6，點關于原點的對稱點為
，直線
交于點
.
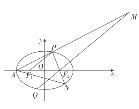
（1）求橢圓方程；
（2）若直線
與橢圓交于另一點
，且
，求點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】 已知函數f(x)＝|x＋a|＋|x－2|.
(1)當a＝－3時，求不等式f(x)≥3的解集；
(2)若f(x)≤|x－4|的解集包含[1，2]，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】《易經》是中國傳統文化中的精髓，如圖是易經八卦（含乾、坤、巽、震、坎、離、艮、兌八卦），每一卦由三根線組成（"
"表示一根陽線，"
"表示一根陰線），從八卦中任取兩卦，這兩卦的六根線中恰有兩根陽線，四根陰線的概率為_______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
年底，湖北省武漢市等多個地區陸續出現感染新型冠狀病毒肺炎的患者，為及時有效地對疫情數據進行流行病學統計分析，某地研究機構針對該地實際情況，根據該地患者是否有武漢旅行史與是否有確診病例接觸史，將新冠肺炎患者分為四類：有武漢旅行史（無接觸史），無武漢旅行史（無接觸史），有武漢旅行史（有接觸史）和無武漢旅行史（有接觸史），統計得到以下相關數據：
有接觸史 | 無接觸史 | 總計 | |
有武漢旅行史 |
| ||
無武漢旅行史 |
| ||
總計 |
|
|
（1）請將上面列聯表填寫完整，并判斷能否在犯錯誤的概率不超過
的前提下，認為有武漢旅行史與有確診病例接觸史有關系？
（2）已知在無武漢旅行史的
名患者中，有
名無癥狀感染者.現在從無武漢旅行史的名患者中，選出名進行病例研究，求人中至少有
名是無癥狀感染者的概率.
下面的臨界值表供參考：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式：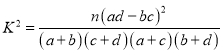
，其中
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
