Question

【題目】現對某市工薪階層關于“樓市限購令”的態度進行調查，隨機抽調了50人，他們月收入的頻數分布及對“樓市限購令”贊成人數如下表.

月收入(單位百元)
頻數	5	10	15	10	5	5
贊成人數	4	8	12	5	2	1

(1)由以上統計數據填下面2×2列聯表，并問是否有99％的把握認為“月收入以5500元為分界點對“樓市限購令”的態度有差異；

	月收入不低于55百元的人數	月收入低于55百元的人數	合計
贊成	a=______________	c=______________	______________
不贊成	b=______________	d=______________	______________
合計	______________	______________	______________

(2)試求從年收入位于（單位：百元）的區間段的被調查者中隨機抽取2人，恰有1位是贊成者的概率。

參考公式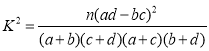：，其中.

參考值表：

	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

Answer 1

【答案】（1）填表見解析，沒有的把握認為月收入以5500元為分界點對“樓市限購令”的態度有差異（2）

【解析】

（1）根據題目所給數據，填寫列聯表.計算，故沒有的把握認為月收入以5500元為分界點對“樓市限購令”的態度有差異.（2）利用列舉法和古典概型概率計算公式，計算出所求概率.

解：（1）列聯表：

	月收入不低于55百元的人數	月收入低于55百元的人數	合計
贊成	a=_________3_____	c=______29________	_______32_______
不贊成	b=___7___________	d=____11__________	__________18____
合計	_____10_________	______40________	_________50_____

則沒有的把握認為月收入以5500元為分界點對“樓市限購令”的態度有差異.

（2）年收入位于（單位：百元）的區間段的被調查者有5人，其中贊成者2人，記為a，b，不贊成者3人，記為A，B，C.

列舉如下：

故所求概率為