
【題目】已知函數![]() .
.
(Ⅰ)求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(Ⅱ)若函數![]() 在區間
在區間![]() 上存在極值,求實數
上存在極值,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)設![]() ,對任意
,對任意![]() 恒有
恒有![]() ,求實數
,求實數![]() 的取值范圍。
的取值范圍。
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)求出導函數得到斜率,利用點斜式得到切線方程;
(Ⅱ)求出函數的極值,再探討函數在區間 (m,m![]() )(其中a>0)上存在極值,尋找關于m的不等式,求出實數m的取值范圍;
)(其中a>0)上存在極值,尋找關于m的不等式,求出實數m的取值范圍;
(Ⅲ)先求導,再構造函數h(x)=lnx![]() ,求出h(x)的最大值小于0即可.
,求出h(x)的最大值小于0即可.
解:(I). ![]()
故切線的斜率為![]() ,又f(e)=
,又f(e)=![]()
∴切線方程為:![]() ,即
,即![]()
(II).當![]() 時,
時,![]()
當x>l時,![]()
f(x)在(0,1)上單調遞增,在(1.+![]() )上單調遞減。
)上單調遞減。
故f(x)在x=l處取得極大值。
∵f(x)在區間(m,m+![]() )(m>0)上存在極值,
)(m>0)上存在極值,
∴0<m<1且m+![]() >1,解得
>1,解得![]()
(Ⅲ).由題可知.a≠0,且![]()
![]() ,
,
![]() ,
,
當a<0時,g(x)>0.不合題意。
當a>0時,由![]() 可得
可得![]() 恒成立
恒成立
設![]() ,則
,則![]()
求導得: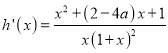
設![]()
①當0<a≤l時,△≤0,此時:![]()
∴h(x)在(0,1)內單調遞增,又h(l)=0,所以h(x)<h(l)=0.
所以0<a≤l符合條件.
②當a>1時,△>0,注意到t(0)=1,t(1)=4(1-a)<0,存在xo![]() (0,1),使得t(x0)=0,
(0,1),使得t(x0)=0,
于是對任意![]() ,t(x)<0,h’(x)<0.則h(x)在(xo,1)內單調遞減,又h(l)=0,所以當
,t(x)<0,h’(x)<0.則h(x)在(xo,1)內單調遞減,又h(l)=0,所以當![]() 時,h(x)>0,不合要求,
時,h(x)>0,不合要求,
綜合①②可得0<a≤1


科目:高中數學 來源: 題型:
【題目】在所有棱長都相等的三棱錐![]() 中,D,E,F分別是AB,BC,CA的中點,下列四個命題:
中,D,E,F分別是AB,BC,CA的中點,下列四個命題:
(1)![]() 平面PDF;(2)
平面PDF;(2)![]() 平面
平面![]() ;
;
(3)平面![]() 平面
平面![]() ;(4)平面
;(4)平面![]() 平面
平面![]() .
.
其中正確命題的序號為________.
A.(2)(3)B.(1)(3)C.(2)(4)D.(1)(4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家具公司生產甲、乙兩種書柜,制柜需先制白胚再油漆,每種柜的制造白胚工時數、油漆工時數的有關數據如下:
工藝要求 | 產品甲 | 產品乙 | 生產能力(工時/天) |
制白胚工時數 | 6 | 12 | 120 |
油漆工時數 | 8 | 4 | 64 |
單位利潤 | 20元 | 24元 |
則該公司合理安排這兩種產品的生產,每天可獲得的最大利潤為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A、B為橢圓![]() (
(![]() )和雙曲線
)和雙曲線![]() 的公共頂點,P、Q分別為雙曲線和橢圓上不同于A、B的動點,且
的公共頂點,P、Q分別為雙曲線和橢圓上不同于A、B的動點,且![]() (
(![]() ,
,![]() ),設AP、BP、AQ、BQ的斜率分別為
),設AP、BP、AQ、BQ的斜率分別為![]() 、
、![]() 、
、![]() 、
、![]() .
.
(1)若![]() ,求
,求![]() 的值(用a、b的代數式表示);
的值(用a、b的代數式表示);
(2)求證:![]() ;
;
(3)設![]() 、
、![]() 分別為橢圓和雙曲線的右焦點,若
分別為橢圓和雙曲線的右焦點,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,離心率為
,離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,且
上,且![]() 的周長為
的周長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知過點![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() 兩點,點
兩點,點![]() 在直線
在直線![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com