
【題目】如圖,在△ABC中,AB⊥AC,若AD⊥BC,則AB2=BD·BC;類似地有命題:在三棱錐A-BCD中,AD⊥平面ABC,若A點在平面BCD內的射影為M,則有S![]() =S△BCM·S△BCD.上述命題是 ( )
=S△BCM·S△BCD.上述命題是 ( )

A. 真命題
B. 增加條件“AB⊥AC”才是真命題
C. 增加條件“M為△BCD的垂心”才是真命題
D. 增加條件“三棱錐A-BCD是正三棱錐”才是真命題
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() ,滿足
,滿足![]() ,
,![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)若關于![]() 的不等式
的不等式![]() 在
在![]() 上有解,求實數
上有解,求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() 的兩個零點分別在區間
的兩個零點分別在區間![]() 和
和![]() 內,求實數
內,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=a-![]() .
.
(1)求f(0);
(2)探究f(x)的單調性,并證明你的結論;
(3)若f(x)為奇函數,求滿足f(ax)<f(2)的x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知M(x1,y1)是橢圓![]() =1(a>b>0)上任意一點,F為橢圓的右焦點.
=1(a>b>0)上任意一點,F為橢圓的右焦點.

(1)若橢圓的離心率為e,試用e,a,x1表示|MF|,并求|MF|的最值;
(2)已知直線m與圓x2+y2=b2相切,并與橢圓交于A、B兩點,且直線m與圓的切點Q在y軸右側,若a=4,求△ABF的周長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】a,b為空間中兩條互相垂直的直線,等腰直角三角形ABC的直角邊AC所在直線與a,b都垂直,斜邊AB以直線AC為旋轉軸旋轉,有下列結論:
①當直線AB與a成60°角時,AB與b成30°角;
②當直線AB與a成60°角時,AB與b成60°角;
③直線AB與a所成角的最小值為45°;
④直線AB與a所成角的最大值為60°.
其中正確的是________.(填寫所有正確結論的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的右頂點、上頂點分別為
的右頂點、上頂點分別為![]() 、
、![]() ,坐標原點到直線
,坐標原點到直線![]() 的距離為
的距離為![]() ,且
,且![]() ,則橢圓
,則橢圓![]() 的方程為( )
的方程為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
寫出直線![]() 的方程,利用原點到直線
的方程,利用原點到直線![]() 的距離,以及
的距離,以及![]() 列方程組,解方程組求得
列方程組,解方程組求得![]() 的值,進而求得橢圓的方程.
的值,進而求得橢圓的方程.
橢圓右頂點坐標為![]() ,上頂點坐標為
,上頂點坐標為![]() ,故直線
,故直線![]() 的方程為
的方程為![]() ,即
,即![]() ,依題意原點到直線的距離為
,依題意原點到直線的距離為![]() ,且
,且![]() ,由此解得
,由此解得![]() ,故橢圓的方程為
,故橢圓的方程為![]() ,故選D.
,故選D.
【點睛】
本小題主要考查過兩點的直線方程,考查點到直線的距離公式,考查橢圓標準方程的求法,考查了方程的思想.屬于中檔題.
【題型】單選題
【結束】
11
【題目】若實數![]() ,
,![]() 滿足
滿足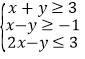 ,則
,則![]() 的最小值是( )
的最小值是( )
A. 0 B. ![]() C. -6 D. -3
C. -6 D. -3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面內動點![]() 到兩定點
到兩定點![]() 和
和![]() 的距離之和為4.
的距離之和為4.
(Ⅰ)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)已知直線![]() 和
和![]() 的傾斜角均為
的傾斜角均為![]() ,直線
,直線![]() 過坐標原點
過坐標原點![]() 且與曲線
且與曲線![]() 相交于
相交于![]() ,
, ![]() 兩點,直線
兩點,直線![]() 過點
過點![]() 且與曲線
且與曲線![]() 是交于
是交于![]() ,
, ![]() 兩點,求證:對任意
兩點,求證:對任意![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com