【題目】設函數
，
，其中
，
為正實數.
（1）若
的圖象總在函數
的圖象的下方，求實數的取值范圍；
（2）設
，證明：對任意，都有
.
【答案】（1）
（2）證明見解析
【解析】
(1)據題意可得
在區間
上恒成立，利用導數討論函數的單調性，從而求出滿足不等式的
的取值范圍；(2)不等式整理為
，由(1)可知當
時，
，利用導數判斷函數
的單調性從而證明
在區間上成立，從而證明對任意
，都有
.
（1）解：因為函數
的圖象恒在
的圖象的下方，
所以
在區間上恒成立.
設
，其中，
所以
，其中
，
.
①當
，即
時，
，
所以函數
在上單調遞增，
，
故
成立，滿足題意.
②當
，即
時，設
，
則
圖象的對稱軸
，
，
，
所以在上存在唯一實根，設為
，則
，
，
，
所以在
上單調遞減，此時
，不合題意.
綜上可得，實數的取值范圍是.
（2）證明：由題意得
，
因為當時，
，
，
所以
.
令
，則
，
所以
在上單調遞增，
，即
，
所以
，從而
.
由（1）知當時，
在上恒成立，整理得.
令
，則要證，只需證
.
因為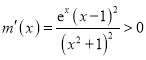
，所以
在上單調遞增，
所以
，即在上恒成立.
綜上可得，對任意，都有成立.
課課練江蘇系列答案
名牌中學課時作業系列答案
明天教育課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案科目：高中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，AB//CD，∠ABD=30°，AB＝2CD＝2AD＝2，DE⊥平面ABCD，EF//BD，且BD＝2EF．
（Ⅰ）求證：平面ADE⊥平面BDEF；
（Ⅱ）若二面角C
BFD的大小為60°，求CF與平面ABCD所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“初中數學靠練，高中數學靠悟”.總結反思自己已經成為數學學習中不可或缺的一部分，為了了解總結反思對學生數學成績的影響，某校隨機抽取200名學生，抽到不善于總結反思的學生概率是0.6.
（1）完成
列聯表（應適當寫出計算過程）；
（2）試運用獨立性檢驗的思想方法分析是否有
的把握認為學生的學習成績與善于總結反思有關.
統計數據如下表所示：
不善于總結反思 | 善于總結反思 | 合計 | |
學習成績優秀 | 40 | ||
學習成績一般 | 20 | ||
合計 | 200 |
參考公式：
其中
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某省新課改后某校為預測2020屆高三畢業班的本科上線情況，從該校上一屆高三（1）班到高三（5）班隨機抽取50人，得到各班抽取的人數和其中本科上線人數，并將抽取數據制成下面的條形統計圖.
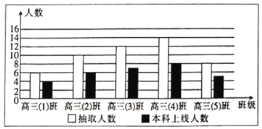
（1）根據條形統計圖，估計本屆高三學生本科上線率.
（2）已知該省甲市2020屆高考考生人數為4萬，假設以（1）中的本科上線率作為甲市每個考生本科上線的概率.
（i）若從甲市隨機抽取10名高三學生，求恰有8名學生達到本科線的概率（結果精確到0.01）；
（ii）已知該省乙市2020屆高考考生人數為3.6萬，假設該市每個考生本科上線率均為
，若2020屆高考本科上線人數乙市的均值不低于甲市，求p的取值范圍.
可能用到的參考數據：取
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中，曲線
是由兩個定點
和點
的距離之積等于
的所有點組成的，對于曲線，有下列四個結論：①曲線是軸對稱圖形；②曲線上所有的點都在單位圓
內；③曲線是中心對稱圖形；④曲線上所有點的縱坐標
.其中，所有正確結論的序號是______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知單調遞增的等比數列
滿足：
.且
是
，
的等差中項.又數列
滿足：
，
，
.
（1）求數列的通項公式；
（2）若
，且數列為等比數列，求
的值；
（3）若
，且
為數列的最小項，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】德國著名數學家狄利克雷(Dirichlet,1805~1859)在數學領域成就顯著.19世紀,狄利克雷定義了一個“奇怪的函數”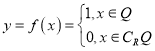 
其中R為實數集,Q為有理數集.則關于函數
有如下四個命題,正確的為( )
A.函數是偶函數
B.
,
,
恒成立
C.任取一個不為零的有理數T,
對任意的
恒成立
D.不存在三個點
,
,
,使得
為等腰直角三角形
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于正整數
，如果
個整數
滿足
，
且
，則稱數組
為的一個“正整數分拆”.記均為偶數的“正整數分拆”的個數為
均為奇數的“正整數分拆”的個數為
.
(Ⅰ)寫出整數4的所有“正整數分拆”;
(Ⅱ)對于給定的整數
，設是的一個“正整數分拆”，且
，求
的最大值;
(Ⅲ)對所有的正整數，證明:
;并求出使得等號成立的的值.
(注:對于的兩個“正整數分拆”與
，當且僅當
且
時，稱這兩個“正整數分拆”是相同的.)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
