
【題目】某外商到一開發區投資72萬美元建起一座蔬菜加工廠,第一年各種經費12萬美元,以后每年增加4萬美元,每年銷售蔬菜收入50萬美元。設![]() 表示前
表示前![]() 年的純收入(
年的純收入(![]() 前
前![]() 年的總收入一前
年的總收入一前![]() 年的總支出一投資額)
年的總支出一投資額)
(1)試寫出![]() 的關系式.
的關系式.
(2) 該開發商從第幾年開始獲利?
【答案】(1)f(n)=﹣2n2+40n﹣72(2)3.
【解析】
(1)根據第一年共支出12萬元,以后每年支出增加4萬元,可知每年的支出構成一個等差數列,故n年的總支出函數關系可用數列的求和公式得到;再根據f(n)=前n年的總收入﹣前n年的總支出﹣投資額,可得前n年的純利潤總和f(n)關于n的函數關系式;(2)令f(n)>0,并解不等式,即可求得該廠從第幾年開始盈利;
解:(1)由題意,第一年共支出12萬元,以后每年支出增加4萬元,可知每年的支出構成一個等差數列,用g(n)表示前n年的總支出,
∴g(n)=12n+![]() ×4=
×4=![]() +10n(n∈N*)
+10n(n∈N*)
∵f(n)=前n年的總收入﹣前n年的總支出﹣投資額
∴f(n)=50n﹣(2n2+10n)﹣72=﹣2n2+40n﹣72.
(2)由(1)知:f(n)=﹣2n2+40n﹣72,
所以當f(n)>0時,即﹣2n2+40n﹣72>0,解得2<n<18.
由n∈N*知,從第三年開始盈利.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】“楊輝三角”是我國數學史上的一個偉大成就,是二項式系數在三角形中的一種幾何排列.如圖所示,去除所有為1的項,依此構成數列2,3,3,4,6,4,5,10,10,5,…,則此數列的前56項和為_____.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解人們對“延遲退休年齡政策”的態度,某部門從年齡在![]() 歲到
歲到![]() 歲的人群中隨機調查了
歲的人群中隨機調查了![]() 人,并得到如圖所示的頻率分布直方圖,在這
人,并得到如圖所示的頻率分布直方圖,在這![]() 人中不支持“延遲退休年齡政策”的人數與年齡的統計結果如圖所示:
人中不支持“延遲退休年齡政策”的人數與年齡的統計結果如圖所示:

年齡 | 不支持“延遲退休年齡政策”的人數 |
|
|
|
|
|
|
|
|
|
|
(1)由頻率分布直方圖,估計這![]() 人年齡的平均數;
人年齡的平均數;
(2)根據以上統計數據填寫下面的![]() 列聯表,據此表,能否在犯錯誤的概率不超過
列聯表,據此表,能否在犯錯誤的概率不超過![]() 的前提下,認為以
的前提下,認為以![]() 歲為分界點的不同人群對“延遲退休年齡政策”的態度存在差異?
歲為分界點的不同人群對“延遲退休年齡政策”的態度存在差異?
45歲以下 | 45歲以上 | 總計 | |
不支持 | |||
支持 | |||
總計 |
附:![]()
參考數據:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖是A,B兩所學校藝術節期間收到的各類藝術作品的情況的統計圖:
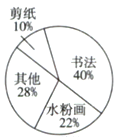

A學校 B學校
(1)從圖中能否看出哪所學校收到的水粉畫作品數量多?為什么?
(2)已知A學校收到的剪紙作品比B學校的多20件,收到的書法作品比B學校的少100件,請問這兩所學校收到藝術作品的總數分別是多少件?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為了了解校園安全教育系列活動的成效,對全市高中生進行一次安全意識測試,根據測試成績評定“合格”、“不合格”兩個等級,同時對相應等級進行量化,現隨機抽取部分高中生的答卷,統計結果如下,對應的頻率分布直方圖如圖所示.
等級 | 不合格 | 合格 | ||
得分 | [20,40) | [40,60) | [60,80) | [80,100) |
頻數 | 12 |
| 48 | 24 |
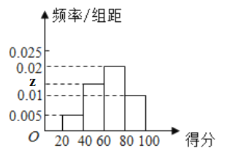
(1)求![]() 、
、![]() 的值;
的值;
(2)估計該市高中生測試成績評定等級為“合格”的概率;
(3)在抽取的答卷中,用分層抽樣的方法,從評定等級為“合格”和“不合格”的答卷中抽取5份,再從這5份答卷中任取2份,求恰有1份評定等級為“不合格”的概率
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人某次飛鏢游戲中的成績如下:甲:8,6,7,7,8,10,9,8,7,8; 乙:9,10,6,7,9,9,10,8,9,10.其中甲的成績可用如圖(1)所示的打點圖(或點狀圖)表示,每個成績上面的點的個數表示這個成績出現的次數.在圖(2)中作出乙的成績的打點圖,并由圖寫出關于甲、乙成績比較的兩個統計結論.

![]()
(1) (2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,已知曲線![]() :
:![]() 和曲線
和曲線![]() :
:![]() ,以極點
,以極點![]() 為坐標原點,極軸為
為坐標原點,極軸為![]() 軸非負半軸建立平面直角坐標系.
軸非負半軸建立平面直角坐標系.
(1)求曲線![]() 和曲線
和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 是曲線
是曲線![]() 上一動點,過點
上一動點,過點![]() 作線段
作線段![]() 的垂線交曲線
的垂線交曲線![]() 于點
于點![]() ,求線段
,求線段![]() 長度的最小值.
長度的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com