Question

【題目】某市為了了解校園安全教育系列活動的成效，對全市高中生進行一次安全意識測試，根據測試成績評定“合格”、“不合格”兩個等級，同時對相應等級進行量化，現隨機抽取部分高中生的答卷，統計結果如下，對應的頻率分布直方圖如圖所示．

等級	不合格		合格
得分	[20，40）	[40，60）	[60，80）	[80，100）
頻數	12		48	24

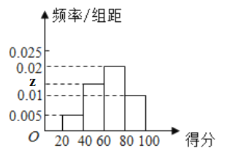
（1）求、的值；

（2）估計該市高中生測試成績評定等級為“合格”的概率；

（3）在抽取的答卷中，用分層抽樣的方法，從評定等級為“合格”和“不合格”的答卷中抽取5份，再從這5份答卷中任取2份，求恰有1份評定等級為“不合格”的概率

Answer 1

【答案】（1），；（2）；（3）．

【解析】

（1）先由圖表求出樣本容量，從而可求出的值，再利用頻率=頻數/樣本容量，求出[40，60）的頻率，再除以組距20就得到的值；

（2）用60分以上的頻數除以樣本容量可得到等級為“合格”的頻率，用此頻率來估計概率即可；

（3）先分層抽樣的性質求出評定等級為“合格”和“不合格”的答卷各為3份，2份，然后列出從5份中抽取2份的所有可能，進而可求出所求的概率.

解：（1）由表格可知樣本容量為

所以，即

由，即

（2）（或）

由此估計該市高中生測試成績等級為“合格”的概率是

（3）合格的有72人、不合格的有48人抽樣比

故從評定等級為“合格”的答卷中抽取的份數為，記為、、

從評定等級為“不合格”的答卷中抽取的份數為，記為、

則從5份答卷中抽取2份，基本事件

共10個基本事件

記事件：恰有1份評定等級為“不合格”

共6個基本事件

則從這5份答卷中抽取2份，恰有1份評定等級為“不合格”的概率為