Question

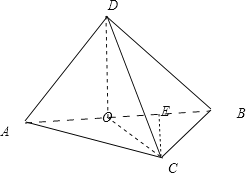
【題目】將一副斜邊長相等的直角三角板拼接成如圖所示的空間圖形，其中，.若將它們的斜邊重合，讓三角形以為軸轉動，則下列說法不正確的是（ ）

A. 當平面平面時，，兩點間的距離為

B. 當平面平面時，與平面所成的角為

C. 在三角形轉動過程中，總有

D. 在三角形轉動過程中，三棱錐的體積最大可達到

Answer 1

【答案】C

【解析】分析：A選項，結合圖象，利用面面垂直的性質及直角三角形斜邊上的中線長等于斜邊長的一半求解；B選項，先作出與平面所成的角，再求得其為；C選項用反證法，假設垂直，根據線面垂直的判定與性質推到是否可能，從而得出結論；D選項根據棱錐的體積公式，在底面積不變的情況下，體積的大小取決于高，當平面ABD⊥平面ABC時，高最大，求出即可．

詳解：A選項，取AB中點O，連接DO、CO，

∵AD=BD=，∴DO=1，AB=2，OC=1

∵平面ABD⊥平面ABC，DO⊥AB，∴DO⊥平面ABC，DO⊥OC，

∴DC=，A選項正確；

B選項，過點D作DM⊥AB，連接MC，則∠DCM就是與平面所成的角，因為DM=CM,所以∠DCM=45°，所以B選項正確；

C選項，若AB⊥CD，則AB⊥平面CDO，AB⊥OC，∵O為中點，∴AC=BC，∠BAC=45°與∠BAC=30°矛盾，∴C選項錯誤；

D選項，當DO⊥平面ABC時，棱錐的高最大，此時V棱錐=×AC×BC×DO=××1×1=．D選項正確．

故答案為：C