
(本小題滿分14分)
已知函數(shù)f (x)=ex,g(x)=lnx,h(x)=kx+b.
(1)當(dāng)b=0時,若對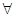 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求實數(shù)k的取值范圍;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求實數(shù)k的取值范圍;
(2)設(shè)h(x)的圖象為函數(shù)f (x)和g(x)圖象的公共切線,切點分別為(x1, f (x1))和(x2, g(x2)),其中x1>0.
①求證:x1>1>x2;
②若當(dāng)x≥x1時,關(guān)于x的不等式ax2-x+xe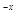 +1≤0恒成立,求實數(shù)a的取值范圍.
+1≤0恒成立,求實數(shù)a的取值范圍.
(1)[ ,e](2)①分別求f(x)和g(x)在點(x1, f (x1))和(x2, g(x2))的切線,記為公切線,所以斜率和截距分別相同,從而得證結(jié)論;②(-∞,1]
,e](2)①分別求f(x)和g(x)在點(x1, f (x1))和(x2, g(x2))的切線,記為公切線,所以斜率和截距分別相同,從而得證結(jié)論;②(-∞,1]
解析試題分析:(1)依題意對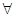 x∈(0,+∞)均有ex≥kx≥lnx成立,
x∈(0,+∞)均有ex≥kx≥lnx成立,
即對任意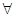 x∈(0,+∞)均有
x∈(0,+∞)均有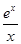 ≥k≥
≥k≥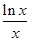 成立, ……1分
成立, ……1分
∴(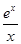 )min≥k≥
)min≥k≥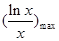 ,
,
因為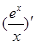 =
= ,故
,故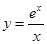 在(0,1)上減,(1,+∞)增,
在(0,1)上減,(1,+∞)增,
∴(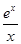 )min=e,
)min=e,
又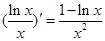 ,故
,故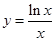 在(0,e)上減,(e,+∞)增,
在(0,e)上減,(e,+∞)增,
∴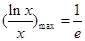 ,即k的取值范圍是[
,即k的取值范圍是[ ,e] . ……5分
,e] . ……5分
(2)由題知:h(x)即為y-e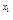 = e
= e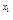 (x-x1)即y=e
(x-x1)即y=e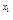 ·x+ e
·x+ e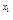 -x1 e
-x1 e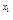 ,
,
也為y=lnx2=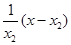 即y=
即y=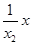 +lnx2-1,
+lnx2-1,
∴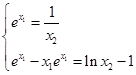 , ……6分
, ……6分
又x1=0 ∴e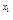 >1 即
>1 即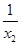 >1
>1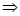 x1>1即x1>1>x2, ……8分
x1>1即x1>1>x2, ……8分
(3)令F(x)=ax2-x+xe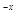 +1(x≥x1),
+1(x≥x1),
∴F′(x)= -1-xe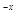 +e
+e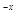 =-1+e
=-1+e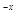 (1-x)( x≥x1)
(1-x)( x≥x1)
又x≥x1>1 F′(x)= -1-xe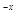 +e
+e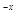 =-1+e
=-1+e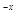 (1-x)<0,
(1-x)<0,
即F(x)=ax2-x+xe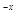 +1(x≥x1)單減,
+1(x≥x1)單減,
所以只要F(x)≤F(x1)= ax2-x1+1xe +1≤0,
+1≤0,
即a+ x1-x1e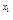 + e
+ e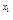 ≤0. ……12分
≤0. ……12分
由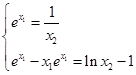 ,
,
∴ ,
,
即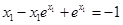
故只要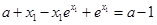 ≤0得:a≤1,
≤0得:a≤1,
綜上,實數(shù)a的取值范圍是(-∞,1]. ……14分
考點:本小題主要考查利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性、極值、最值等和利用導(dǎo)數(shù)求曲線的切線,和利用導(dǎo)數(shù)解決恒成立問題,考查學(xué)生綜合運算所學(xué)知識分析問題、解決問題的能力和運算求解能力.
點評:導(dǎo)數(shù)是研究函數(shù)性質(zhì)的有力工具,要熟練應(yīng)用,而恒成立問題一般要轉(zhuǎn)化為最值問題解決.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
已知區(qū)間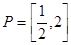 ,函數(shù)
,函數(shù) 的定義域為
的定義域為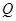
(1)若函數(shù)在區(qū)間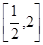 上是增函數(shù),求實數(shù)
上是增函數(shù),求實數(shù) 的取值范圍
的取值范圍
(2)若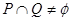 ,求實數(shù)
,求實數(shù) 的取值范圍
的取值范圍
(3)若關(guān)于 的方程
的方程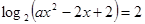 在區(qū)間
在區(qū)間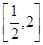 內(nèi)有解,求實數(shù)
內(nèi)有解,求實數(shù) 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分12分)
設(shè)函數(shù)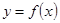 滿足:對任意的實數(shù)
滿足:對任意的實數(shù)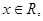 有
有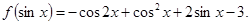
(Ⅰ)求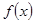 的解析式;
的解析式;
(Ⅱ)若方程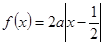 有解,求實數(shù)
有解,求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(滿分12分)
某市居民生活用水標(biāo)準(zhǔn)如下:
| 用水量t(單位:噸) | 每噸收費標(biāo)準(zhǔn)(單位:元) |
| 不超過2噸部分 | m |
| 超過2噸不超過4噸部分 | 3 |
| 超過4噸部分 | n |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在經(jīng)濟(jì)學(xué)中,函數(shù) 的邊際函數(shù)
的邊際函數(shù)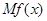 定義為
定義為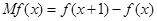 .某公司每月最多生產(chǎn)100臺報警系統(tǒng)裝置,生產(chǎn)
.某公司每月最多生產(chǎn)100臺報警系統(tǒng)裝置,生產(chǎn)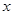 臺(
臺(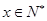 )的收入函數(shù)為
)的收入函數(shù)為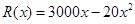 (單位:元),其成本函數(shù)為
(單位:元),其成本函數(shù)為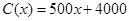 (單位:元),利潤是收入與成本之差.
(單位:元),利潤是收入與成本之差.
(1)求利潤函數(shù)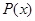 及邊際利潤函數(shù)
及邊際利潤函數(shù)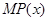 的解析式,并指出它們的定義域;
的解析式,并指出它們的定義域;
(2)利潤函數(shù)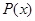 與邊際利潤函數(shù)
與邊際利潤函數(shù)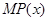 是否具有相同的最大值?說明理由;
是否具有相同的最大值?說明理由;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分13分)
已知函數(shù)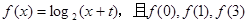 成等差數(shù)列,點
成等差數(shù)列,點 是函數(shù)
是函數(shù) 圖像上任意一點,點
圖像上任意一點,點 關(guān)于原點的對稱點
關(guān)于原點的對稱點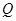 的軌跡是函數(shù)
的軌跡是函數(shù)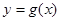 的圖像。
的圖像。
(1)解關(guān)于 的不等式
的不等式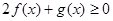 ;
;
(2)當(dāng)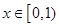 時,總有
時,總有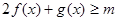 恒成立,求
恒成立,求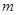 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
已知函數(shù)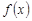 =
=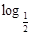 (ex-1)。
(ex-1)。
(1)求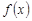 的定義域;
的定義域;
(2)判斷函數(shù)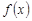 的增減性,并用定義法證明.
的增減性,并用定義法證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12)
為了綠化城市,準(zhǔn)備在如圖所示的區(qū)域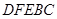 內(nèi)修建一個矩形
內(nèi)修建一個矩形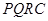 的草坪,并建立如圖平面直角坐標(biāo)系,且
的草坪,并建立如圖平面直角坐標(biāo)系,且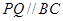 ,
,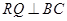 ,另外
,另外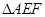 的內(nèi)部有一文物保護(hù)區(qū)不能占用,經(jīng)測量
的內(nèi)部有一文物保護(hù)區(qū)不能占用,經(jīng)測量 ,
,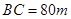 ,
, 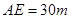 ,
,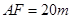 .
.
(1)求直線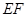 的方程;
的方程;
(2)應(yīng)如何設(shè)計才能使草坪的占地面積最大?并求最大面積。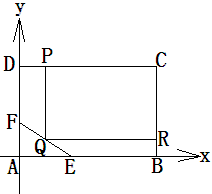
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com