
【題目】高鐵和航空的飛速發展不僅方便了人們的出行,更帶動了我國經濟的巨大發展,據統計,在2018年這一年內從A市到B市乘坐高鐵或飛機出行的成年人約為50萬人次.為了解乘客出行的滿意度,現從中隨機抽取100人次作為樣本.得到下表(單位:人次):
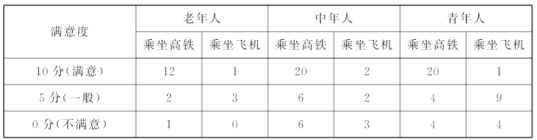
(1)在樣本中任取1個,求這個出行人恰好不是青年人的概率;
(2)在2018年從A市到B市乘坐高鐵的所有成年人中,隨機選取2人次,記其中老年人出行的人次為X.以頻率作為概率.求X的分布列和數學期望;
(3)如果甲將要從A市出發到B市,那么根據表格中的數據,你建議甲是乘坐高鐵還是 飛機?并說明理由.
【答案】(1)![]() (2)見解析(3)乘坐高鐵,見解析
(2)見解析(3)乘坐高鐵,見解析
【解析】
(1)根據分層抽樣的特征可以得知,樣本中出行的老年人、中年人、青年人人次分別為19,39,42,即可按照古典概型的概率計算公式計算得出;
(2)依題意可知![]() 服從二項分布,先計算出隨機選取1人次,此人為老年人概率是
服從二項分布,先計算出隨機選取1人次,此人為老年人概率是![]() ,所以
,所以![]() ,即
,即![]() ,即可求出
,即可求出![]() 的分布列和數學期望;
的分布列和數學期望;
(3)可以計算滿意度均值來比較乘坐高鐵還是飛機.
(1)設事件:“在樣本中任取1個,這個出行人恰好不是青年人”為![]() ,
,
由表可得:樣本中出行的老年人、中年人、青年人人次分別為19,39,42,
所以在樣本中任取1個,這個出行人恰好不是青年人的概率![]() ;
;
(2)由題意,![]() 的所有可能取值為:0,1,2,
的所有可能取值為:0,1,2,
因為在2018年從![]() 市到
市到![]() 市乘坐高鐵的所有成年人中,隨機選取1人次,此人
市乘坐高鐵的所有成年人中,隨機選取1人次,此人
為老年人概率是![]() ,
,
所以![]() ,
,
![]() ,
,
![]() ,
,
所以隨機變量![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 |
|
|
|
|
故![]() ;
;
(3)從滿意度的均值來分析問題如下:
由表可知,乘坐高鐵的人滿意度均值為:![]() ,
,
乘坐飛機的人滿意度均值為:![]() ,
,
因為![]() ,
,
所以建議甲乘坐高鐵從![]() 市到
市到![]() 市.
市.


 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案科目:高中數學 來源: 題型:
【題目】選修![]() :不等式選講
:不等式選講
已知函數f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若關于x的不等式f(x)≤|3m+1|有解,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校舉行運動會,其中三級跳遠的成績在![]() 米以上的進入決賽,把所得的成績進行整理后,分成
米以上的進入決賽,把所得的成績進行整理后,分成![]() 組畫出頻率分布直方圖的一部分(如圖),已知第
組畫出頻率分布直方圖的一部分(如圖),已知第![]() 組的頻數是
組的頻數是![]() .
.
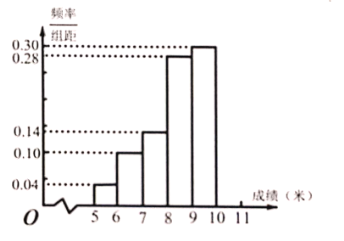
(1)求進入決賽的人數;
(2)用樣本的頻率代替概率,記![]() 表示兩人中進入決賽的人數,求
表示兩人中進入決賽的人數,求![]() 得分布列及數學期望.
得分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《周髀算經》中給出了勾股定理的絕妙證明.如圖是趙爽弦圖及注文.弦圖是一個以勾股形之弦為邊的正方形,其面積稱為弦實.圖中包含四個全等的勾股形及一個小正方形,分別涂成朱色及黃色,其面積稱為朱實、黃實.由2×勾×股+(股-勾)2=4×朱實+黃實=弦實,化簡得勾2+股2=弦2.若圖中勾股形的勾股比為![]() ,向弦圖內隨機拋擲100顆圖釘(大小忽略不計),則落在黃色圖形內的圖釘顆數大約為( )(參考數據:
,向弦圖內隨機拋擲100顆圖釘(大小忽略不計),則落在黃色圖形內的圖釘顆數大約為( )(參考數據:![]() ,
,![]() )
)
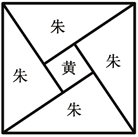
A.2B.4C.6D.8
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某地某月1日至15日的日平均溫度變化的折線圖,根據該折線圖,下列結論正確的是( )
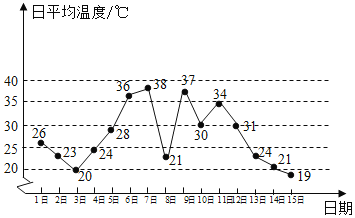
A. 這15天日平均溫度的極差為![]()
B. 連續三天日平均溫度的方差最大的是7日,8日,9日三天
C. 由折線圖能預測16日溫度要低于![]()
D. 由折線圖能預測本月溫度小于![]() 的天數少于溫度大于
的天數少于溫度大于![]() 的天數
的天數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四邊形
,四邊形![]() 為矩形,
為矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值;
所成銳二面角的余弦值;
(Ⅲ)在線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,若存在,求出線段
,若存在,求出線段![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】依照某發展中國家2018年的官方資料,將該國所有家庭按年收入從低到高的順序平均分為五組,依次為第一組至第五組,各組家庭的年收入總和占該國全部家庭的年收入總和的百分比如圖所示.
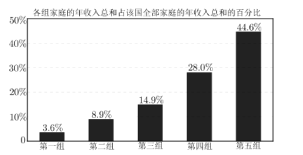
以下關于該國2018年家庭收入的判斷,一定正確的是( )
A. 至少有![]() 的家庭的年收入都低于全部家庭的平均年收入
的家庭的年收入都低于全部家庭的平均年收入
B. 收入最低的那![]() 的家庭平均年收入為全部家庭平均年收入的
的家庭平均年收入為全部家庭平均年收入的![]()
C. 收入最高的那![]() 的家庭年收入總和超過全部家庭年收入總和的
的家庭年收入總和超過全部家庭年收入總和的![]()
D. 收入最低的那![]() 的家庭年收入總和超過全部家庭年收入總和的
的家庭年收入總和超過全部家庭年收入總和的![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點![]() ,
,![]() ,直線
,直線![]() 、
、![]() 相交于點
相交于點![]() ,且它們的斜率之積為
,且它們的斜率之積為![]() ,記動點
,記動點![]() 的軌跡為曲線
的軌跡為曲線![]() 。
。
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 、
、![]() 兩點,是否存在定點
兩點,是否存在定點![]() ,使得直線
,使得直線![]() 與
與![]() 斜率之積為定值,若存在,求出
斜率之積為定值,若存在,求出![]() 坐標;若不存在,請說明理由。
坐標;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 過點
過點![]() ,傾斜角為
,傾斜角為![]() ,在以坐標原點為極點,
,在以坐標原點為極點,![]() 軸的非負半軸為極軸的極坐標系中,曲線
軸的非負半軸為極軸的極坐標系中,曲線![]() 的方程為
的方程為![]() .
.
(1)寫出直線![]() 的參數方程和曲線
的參數方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,設點
兩點,設點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com