【題目】在直角坐標系
中，曲線
的參數方程為
（
為參數）.以坐標原點為極點，
軸的非負半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（Ⅰ）將的方程化為普通方程，將的方程化為直角坐標方程；
（Ⅱ）已知直線
的參數方程為
，
為參數，且
，與交于點
，與交于點
，且
，求
的值.
科目：高中數學 來源： 題型：
【題目】[選修4-4：坐標系與參數方程]
在平面直角坐標系
中，直線
的參數方程為
（
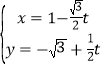為參數），以坐標原點為極點，
軸的非負半軸為極軸，建立極坐標系，曲線
的極坐標方程為
．
（1）求直線的普通方程及曲線的直角坐標方程；
（2）設點
，直線與曲線相交于兩點
，
，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】研究機構對某校學生往返校時間的統計資料表明：該校學生居住地到學校的距離
（單位：千米）和學生花費在上學路上的時間
（單位：分鐘）有如下的統計資料：
到學校的距離 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花費的時間 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果統計資料表明與有線性相關關系，試求：
（1）判斷與是否有很強的線性相關性？
（相關系數
的絕對值大于0.75時，認為兩個變量有很強的線性相關性，精確到0.01）
（2）求線性回歸方程
（精確到0.01）；
（3）將
分鐘的時間數據
稱為美麗數據，現從這6個時間數據中任取2個，求抽取的2個數據全部為美麗數據的概率.
參考數據：
，
，
，
，
，
參考公式：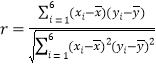
，
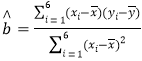
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】圓錐
如圖①所示，圖②是它的正(主)視圖．已知圓
的直徑為
， 
是圓周上異于
的一點， 
為
的中點．
(I)求該圓錐的側面積S；
(II)求證：平面
⊥平面
；
(III)若∠CAB＝60°，在三棱錐
中，求點
到平面
的距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知
，B為AC的中點，分別以AB，AC為直徑在AC的同側作半圓，M，N分別為兩半圓上的動點
不含端點A，B，
，且
，則
的最大值為______．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知變量
、
之間的線性回歸方程為
，且變量、之間的一-組相關數據如下表所示，則下列說法錯誤的是（ ）
|
|
|
|
|
|
|
|
|
|
A.可以預測，當
時，
B.
C.變量之間呈負相關關系D.該回歸直線必過點
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，某人工景觀湖外圍有兩條相互垂直的直線型公路ll，l2，且ll和l2交于點O．為了方便游客游覽，計劃修建一條連接公路與景觀湖的直線型公路AB．景觀湖的輪廓可以近似看成一個圓心為O，半徑為2百米的圓，且公路AB與圓O相切，圓心O到ll，l2的距離均為5百米，設OAB＝
，AB長為L百米．
（1）求L關于的函數解析式；
（2）當為何值時，公路AB的長度最短？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知命題p：x2+mx+1=0有兩個不等的負根；命題q：4x2+4（m﹣2）x+1=0無實根．若命題p與命題q有且只有一個為真，求實數m的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
