
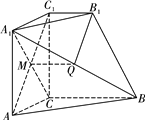
【題目】如圖,在幾何體![]() 中,平面
中,平面![]() 底面ABC,四邊形
底面ABC,四邊形![]() 是正方形,
是正方形,![]() ,Q是
,Q是![]() 的中點,且
的中點,且![]() ,
,![]() .
.

![]() 求證:
求證:![]() 平面
平面![]() ;
;
![]() 求二面角
求二面角![]() 的余弦值.
的余弦值.
【答案】(1)詳見解析;(2)![]() .
.
【解析】
(1)連接![]() ,
,![]() 交于
交于![]() 點,連接
點,連接![]() ,則四邊形
,則四邊形![]() 是正方形,點
是正方形,點![]() 是
是![]() 的中點,推導出四邊形
的中點,推導出四邊形![]() 是平行四邊形,從而
是平行四邊形,從而![]() ,由此能證明
,由此能證明![]() 平面
平面![]() .
.
(2)以![]() 為原點,
為原點,![]() ,
,![]() 分別為
分別為![]() 軸和
軸和![]() 軸建立空間直角坐標系,利用向量法能求出二面角
軸建立空間直角坐標系,利用向量法能求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
證明:(1)如圖所示,連接![]() ,
,![]() 交于
交于![]() 點,連接
點,連接![]() .
.
因為四邊形![]() 是正方形,所以點
是正方形,所以點![]() 是
是![]() 的中點,
的中點,
又已知點![]() 是
是![]() 的中點,所以
的中點,所以![]() ,且
,且![]() ,
,
又因為![]() ,且
,且![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以四邊形![]() 是平行四邊形,故
是平行四邊形,故![]() ,
,
因![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() .
.
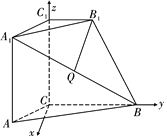
(2)如圖所示,以![]() 為原點,
為原點,![]() 分別為
分別為![]() 軸和
軸和![]() 軸建立空間直角坐標系,
軸建立空間直角坐標系,
不妨設![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
設平面![]() 的法向量為
的法向量為![]() ,
,
則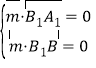 即
即![]() ,取
,取![]() ,則
,則![]()
平面![]() 的一個法向量
的一個法向量![]() ,所以
,所以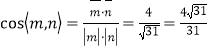 .
.
故二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知圓![]() ,定點
,定點![]() ,
,![]() 為圓上任意一點,線段
為圓上任意一點,線段![]() 的垂直平分線
的垂直平分線![]() 和半徑
和半徑![]() 相交于點
相交于點![]() ,當點
,當點![]() 在圓上運動時,點
在圓上運動時,點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若過定點![]() 的直線交曲線
的直線交曲線![]() 于不同的兩點
于不同的兩點![]() ,
,![]() (點
(點![]() 在點
在點![]() ,
,![]() 之間),且滿足
之間),且滿足![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對數函數g(x)=1ogax(a>0,a≠1)和指數函數f(x)=ax(a>0,a≠1)互為反函數.已知函數f(x)=3x,其反函數為y=g(x).
(Ⅰ)若函數g(kx2+2x+1)的定義域為R,求實數k的取值范圍;
(Ⅱ)若0<x1<x2且|g(x1)|=|g(x2)|,求4x1+x2的最小值;
(Ⅲ)定義在I上的函數F(x),如果滿足:對任意x∈I,總存在常數M>0,都有-M≤F(x)≤M成立,則稱函數F(x)是I上的有界函數,其中M為函數F(x)的上界.若函數h(x)=![]() ,當m≠0時,探求函數h(x)在x∈[0,1]上是否存在上界M,若存在,求出M的取值范圍,若不存在,請說明理由.
,當m≠0時,探求函數h(x)在x∈[0,1]上是否存在上界M,若存在,求出M的取值范圍,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個袋中有4個大小相同的小球,其中紅球1個,白球2個,黑球1個,現從袋中有放回地取球,每次隨機取一個,求
(1)連續取兩次都是白球的概率;
(2)若取一個紅球記2分,取一個白球記1分,取一個黑球記0分,連續取三次分數之和為4分的概率.(本小題基本事件總數較多不要求列舉,但是所求事件含的基本事件要列舉)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】今天你低碳了嗎?近來國內網站流行一種名為“碳排放計算器”的軟件,人們可以由此計算出自己每天的碳排放量,如家居用電的碳排放量(千克)![]() 耗電度數
耗電度數![]() ,汽車的碳排放量(千克)
,汽車的碳排放量(千克)![]() 油耗公升數
油耗公升數![]() 等,某班同學利用寒假在兩個小區逐戶進行了一次生活習慣是否符合低碳觀念的調查.若生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,這二族人數占各自小區總人數的比例
等,某班同學利用寒假在兩個小區逐戶進行了一次生活習慣是否符合低碳觀念的調查.若生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,這二族人數占各自小區總人數的比例![]() 數據如下:
數據如下:
| 低碳族 | 非低碳族 |
| 低碳族 | 非低碳族 | |
比例 | 1/2 | 1/2 | 比例 | 4/5 | 1/5 |
(1)如果甲、乙來自![]() 小區,丙、丁來自
小區,丙、丁來自![]() 小區,求這4人中恰好有兩人是低碳族的概率;
小區,求這4人中恰好有兩人是低碳族的概率;
(2)![]() 小區經過大力宣傳,每周非低碳中有20%的人加入到低碳族的行列,如果兩周后隨機地從
小區經過大力宣傳,每周非低碳中有20%的人加入到低碳族的行列,如果兩周后隨機地從![]() 小區中任選5個人,記
小區中任選5個人,記![]() 表示5個人中的低碳族人數,求
表示5個人中的低碳族人數,求![]() 和
和![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某產品在3-7月份銷售量與利潤的統計數據如下表:
月份 | 3 | 4 | 5 | 6 | 7 |
銷售量 | 3 | 6 | 4 | 7 | 8 |
利潤 | 19 | 34 | 26 | 41 | 46 |
(1)從這5個月的利潤中任選2個值,分別記為![]() ,求事件“
,求事件“![]() 均小于45”的概率;
均小于45”的概率;
(2)已知銷售量![]() 與利潤
與利潤![]() 大致滿足線性相關關系,請根據前4個月的數據,求出
大致滿足線性相關關系,請根據前4個月的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的利潤的估計數據與真實數據誤差不超過2萬元,則認為得到的利潤估計是理想的.請用表格中7月份的數據檢驗由(2)中回歸方程所得的該月的利潤的估計數據是否理想?
參考公式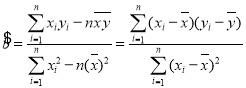 ,
, ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com