
【題目】2018年3月3日至20日中華人民共和國第十三屆全國人民代表大會(huì)第一次會(huì)議和中國人民政治協(xié)商會(huì)議第十三屆全國委員會(huì)第一次會(huì)議在北京勝利召開,兩會(huì)是年度中國政治生活中的一件大事,受到了舉國上下和全世界的廣泛關(guān)注.為及時(shí)宣傳國家政策,貫徹兩會(huì)精神,某校舉行了全國兩會(huì)知識(shí)競賽,為了解本次競賽成績情況,隨機(jī)抽取了部分學(xué)生的成績(得分均為整數(shù),滿分![]() 分,最低分不低于
分,最低分不低于![]() 分)進(jìn)行統(tǒng)計(jì),得出頻率分布表如下:
分)進(jìn)行統(tǒng)計(jì),得出頻率分布表如下:
組號(hào) | 分組 | 頻數(shù) | 頻率 |
第1組 |
|
|
|
第2組 |
|
|
|
第3組 |
|
|
|
第4組 |
|
|
|
第5組 |
|
|
|
合計(jì) |
|
| |
(1)求表中![]() 、
、![]() 、
、![]() 、
、![]() 的值;
的值;
(2)若從成績較好的第![]() 、
、![]() 、
、![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 人擔(dān)任兩會(huì)知識(shí)宣傳員,再從這
人擔(dān)任兩會(huì)知識(shí)宣傳員,再從這![]() 人中隨機(jī)選出
人中隨機(jī)選出![]() 人負(fù)責(zé)整理兩會(huì)相關(guān)材料,求這
人負(fù)責(zé)整理兩會(huì)相關(guān)材料,求這![]() 人中至少有
人中至少有![]() 人來自第
人來自第![]() 組的概率.
組的概率.
【答案】(1)見解析;(2)![]()
【解析】分析:(1)由頻率分布表得:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)由題意可得第![]() 、
、![]() 、
、![]() 組應(yīng)分別抽取
組應(yīng)分別抽取![]() 人、
人、![]() 人、
人、![]() 人.則從
人.則從![]() 為同學(xué)中抽
為同學(xué)中抽![]() 為同學(xué)有
為同學(xué)有![]() 種可能,其中第
種可能,其中第![]() 組至少有
組至少有![]() 人入選有
人入選有![]() 種,則這
種,則這![]() 人中至少有
人中至少有![]() 人來自第
人來自第![]() 組的概率為
組的概率為![]() .
.
詳解:(1)由頻率分布表得:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)∵第![]() 、
、![]() 、
、![]() 組共有
組共有![]() 名學(xué)生,
名學(xué)生,
∴利用分層抽樣在![]() 名學(xué)生中抽取
名學(xué)生中抽取![]() 名學(xué)生,每組分別為:
名學(xué)生,每組分別為:
第![]() 組:
組:![]() 人,第4組:
人,第4組:![]() 人,第5組:
人,第5組:![]() 人,
人,
∴第![]() 、
、![]() 、
、![]() 組應(yīng)分別抽取
組應(yīng)分別抽取![]() 人、
人、![]() 人、
人、![]() 人.
人.
記第![]() 組的
組的![]() 位同學(xué)為
位同學(xué)為![]() ,第
,第![]() 組的
組的![]() 位同學(xué)為
位同學(xué)為![]() 、
、![]() ,第
,第![]() 組的
組的![]() 位同學(xué)為
位同學(xué)為![]() 、
、![]() 、
、![]() ,則從
,則從![]() 為同學(xué)中抽
為同學(xué)中抽![]() 為同學(xué)有
為同學(xué)有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 種可能,
種可能,
其中第![]() 組至少有
組至少有![]() 人入選的有
人入選的有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 種,
種,
∴這![]() 人中至少有
人中至少有![]() 人來自第
人來自第![]() 組的概率為
組的概率為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在如圖所示的幾何體中,![]() 平面
平面![]() .
.
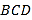
(1)證明:![]() 平面
平面![]() ;
;
(2)過點(diǎn)![]() 作一平行于平面
作一平行于平面![]() 的截面,畫出該截面,說明理由,并求夾在該截面與平面
的截面,畫出該截面,說明理由,并求夾在該截面與平面![]() 之間的幾何體的體積.
之間的幾何體的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側(cè)面
中,側(cè)面![]() 為鈍角三角形且垂直于底面
為鈍角三角形且垂直于底面![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若直線![]() 與底面
與底面![]() 所成的角為60°,求二面角
所成的角為60°,求二面角![]() 余弦值.
余弦值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】現(xiàn)拋擲兩枚骰子,記事件![]() 為“朝上的2個(gè)數(shù)之和為偶數(shù)”,事件
為“朝上的2個(gè)數(shù)之和為偶數(shù)”,事件![]() 為“朝上的2個(gè)數(shù)均為偶數(shù)”,則
為“朝上的2個(gè)數(shù)均為偶數(shù)”,則![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 及函數(shù)
及函數(shù)![]() (a,b,c∈R),若a>b>c且a+b+c=0.
(a,b,c∈R),若a>b>c且a+b+c=0.
(1)證明:f(x)的圖像與g(x)的圖像一定有兩個(gè)交點(diǎn);
(2)請(qǐng)用反證法證明:![]() ;
;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函![]() 數(shù)是奇函數(shù),且f(2)=
數(shù)是奇函數(shù),且f(2)=![]() .
.
(1)求實(shí)數(shù)m和n的值;
(2)求函數(shù)f(x)在區(qū)間[-2,-1]上的最值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市疾控中心流感監(jiān)測結(jié)果顯示,自![]() 年
年![]() 月起,該市流感活動(dòng)一度出現(xiàn)上升趨勢(shì),尤其是
月起,該市流感活動(dòng)一度出現(xiàn)上升趨勢(shì),尤其是![]() 月以來,呈現(xiàn)快速增長態(tài)勢(shì),截止目前流感病毒活動(dòng)度仍處于較高水平,為了預(yù)防感冒快速擴(kuò)散,某校醫(yī)務(wù)室采取積極方式,對(duì)感染者進(jìn)行短暫隔離直到康復(fù).假設(shè)某班級(jí)已知
月以來,呈現(xiàn)快速增長態(tài)勢(shì),截止目前流感病毒活動(dòng)度仍處于較高水平,為了預(yù)防感冒快速擴(kuò)散,某校醫(yī)務(wù)室采取積極方式,對(duì)感染者進(jìn)行短暫隔離直到康復(fù).假設(shè)某班級(jí)已知![]() 位同學(xué)中有
位同學(xué)中有![]() 位同學(xué)被感染,需要通過化驗(yàn)血液來確定感染的同學(xué),血液化驗(yàn)結(jié)果呈陽性即為感染,呈陰性即未被感染.下面是兩種化驗(yàn)方法: 方案甲:逐個(gè)化驗(yàn),直到能確定感染同學(xué)為止;
位同學(xué)被感染,需要通過化驗(yàn)血液來確定感染的同學(xué),血液化驗(yàn)結(jié)果呈陽性即為感染,呈陰性即未被感染.下面是兩種化驗(yàn)方法: 方案甲:逐個(gè)化驗(yàn),直到能確定感染同學(xué)為止;
方案乙:先任取![]() 個(gè)同學(xué),將它們的血液混在一起化驗(yàn),若結(jié)果呈陽性則表明感染同學(xué)為這
個(gè)同學(xué),將它們的血液混在一起化驗(yàn),若結(jié)果呈陽性則表明感染同學(xué)為這![]() 位中的
位中的![]() 位,后再逐個(gè)化驗(yàn),直到能確定感染同學(xué)為止;若結(jié)果呈陰性則在另外
位,后再逐個(gè)化驗(yàn),直到能確定感染同學(xué)為止;若結(jié)果呈陰性則在另外![]() 位同學(xué)中逐個(gè)檢測;
位同學(xué)中逐個(gè)檢測;
(1)求依方案甲所需化驗(yàn)次數(shù)等于方案乙所需化驗(yàn)次數(shù)的概率;
(2)![]() 表示依方案甲所需化驗(yàn)次數(shù),
表示依方案甲所需化驗(yàn)次數(shù),![]() 表示依方案乙所需化驗(yàn)次數(shù),假設(shè)每次化驗(yàn)的費(fèi)用都相同,請(qǐng)從經(jīng)濟(jì)角度考慮那種化驗(yàn)方案最佳.
表示依方案乙所需化驗(yàn)次數(shù),假設(shè)每次化驗(yàn)的費(fèi)用都相同,請(qǐng)從經(jīng)濟(jì)角度考慮那種化驗(yàn)方案最佳.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在正方形![]() 中,點(diǎn)
中,點(diǎn)![]() ,
,![]() 分別為邊
分別為邊![]() ,
,![]() 的中點(diǎn),將
的中點(diǎn),將![]() 沿
沿![]() 所在直線進(jìn)行翻折,將
所在直線進(jìn)行翻折,將![]() 沿
沿![]() 所在直線進(jìn)行翻折,在翻折的過程中,
所在直線進(jìn)行翻折,在翻折的過程中,
①點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 在某一位置可能重合;②點(diǎn)
在某一位置可能重合;②點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 的最大距離為
的最大距離為![]() ;
;
③直線![]() 與直線
與直線![]() 可能垂直; ④直線
可能垂直; ④直線![]() 與直線
與直線![]() 可能垂直.
可能垂直.
以上說法正確的個(gè)數(shù)為( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一個(gè)透明密閉的正方體容器中,恰好盛有該容器一半容積的水,任意轉(zhuǎn)動(dòng)這個(gè)正方體,則水面在容器中的形狀可以是:(1)三角形;(2)長方形;(3)正方形;(4)正六邊形.其中正確的結(jié)論是____________.(把你認(rèn)為正確的序號(hào)都填上)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com