
【題目】已知![]() 為拋物線
為拋物線![]() 上的一點,
上的一點,![]() ,
,![]() 為拋物線上異于點
為拋物線上異于點![]() 的兩點,且直線
的兩點,且直線![]() 的斜率與直線
的斜率與直線![]() 的斜率互為相反數.
的斜率互為相反數.
(1)求直線![]() 的斜率;
的斜率;
(2)設直線![]() 過點
過點![]() 并交拋物線于
并交拋物線于![]() ,
,![]() 兩點,且
兩點,且![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,試探究
,試探究![]() 與
與![]() 的夾角是否為定值,若是則求出定值,若不是,說明理由.
的夾角是否為定值,若是則求出定值,若不是,說明理由.
【答案】(1)![]() ; (2)是定值,
; (2)是定值,![]()
【解析】
(1)根據點![]() 的坐標求出拋物線方程,設出點
的坐標求出拋物線方程,設出點![]() 和點
和點![]() 的坐標,利用斜率公式和拋物線方程,求出
的坐標,利用斜率公式和拋物線方程,求出![]() 和
和![]() ,再根據
,再根據![]() 和
和![]() 互為相反數,得到
互為相反數,得到![]() ,進而求出直線
,進而求出直線![]() 的斜率;
的斜率;
(2)設出點![]() 和點
和點![]() 的坐標,根據
的坐標,根據![]() ,得到
,得到![]() ,再設出直線
,再設出直線![]() 的方程,與拋物線聯立,利用韋達定理,并結合
的方程,與拋物線聯立,利用韋達定理,并結合![]() ,化簡
,化簡![]() ,得到
,得到![]() 的坐標表示,求出
的坐標表示,求出![]() ,借助向量的數量積,即可求得
,借助向量的數量積,即可求得![]() 與
與![]() 的夾角.
的夾角.
(1)設![]() ,
,![]() ,
,
因為點![]() 為拋物線
為拋物線![]() 上的一點,
上的一點,
所以![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
同時,有![]() ,
,![]() ,
,
![]() ,
,
同理,![]() ,
,
因為直線![]() 的斜率與直線
的斜率與直線![]() 的斜率互為相反數,
的斜率互為相反數,
所以![]() ,即
,即![]() ,
,
故![]() .
.
(2)設直線![]() 的方程為
的方程為![]() ,
,![]() ,
,![]() ,
,![]() ,
,
將直線![]() 的方程代入
的方程代入![]() ,得
,得![]() ,
,
所以![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,且
,且![]() ,
,
![]()
![]() ,解得
,解得![]() ,
,
![]()
![]()
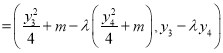 ,
,
又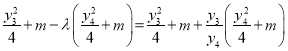
![]()
![]()
![]() ,
,
![]()
![]() ,
,
又![]() ,
,![]()
![]() ,
,
![]()
![]() ,即
,即![]() 與
與![]() 的夾角為
的夾角為![]() .
.
![]()
![]() 與
與![]() 的夾角是定值,定值為
的夾角是定值,定值為![]() .
.


 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C的參數方程為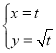 (t為參數),點A(1,0),B(3,
(t為參數),點A(1,0),B(3,![]() ),若以直角坐標系xOy的O點為極點,x軸正方向為極軸,且長度單位相同,建立極坐標系.
),若以直角坐標系xOy的O點為極點,x軸正方向為極軸,且長度單位相同,建立極坐標系.
(1)求直線AB的極坐標方程;
(2)求直線AB與曲線C交點的極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,點
,點![]() ,
,![]() ,
,![]() 分別為橢圓的左焦點、右頂點和下頂點,
分別為橢圓的左焦點、右頂點和下頂點,![]() 的面積為
的面積為![]() ,且橢圓的離心率為
,且橢圓的離心率為![]() .
.
(1)求橢圓的標準方程;
(2)若點![]() 為橢圓
為橢圓![]() 上一點,直線
上一點,直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,
,![]() ,且
,且![]() (點
(點![]() 為坐標原點),求
為坐標原點),求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】BMI指數(身體質量指數,英文為BodyMassIndex,簡稱BMI)是衡量人體胖瘦程度的一個標準,BMI=體重(kg)/身高(m)的平方.根據中國肥胖問題工作組標準,當BMI≥28時為肥胖.某地區隨機調查了1200名35歲以上成人的身體健康狀況,其中有200名高血壓患者,被調查者的頻率分布直方圖如下:
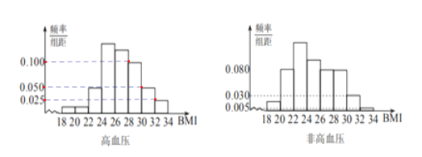
(1)求被調查者中肥胖人群的BMI平均值![]() ;
;
(2)填寫下面列聯表,并判斷是否有99.9%的把握認為35歲以上成人患高血壓與肥胖有關.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
肥胖 | 不肥胖 | 合計 | |
高血壓 | |||
非高血壓 | |||
合計 |
附: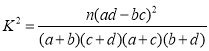 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,
,![]() ,
,![]() ,給出以下四個命題:①
,給出以下四個命題:①![]() 為偶函數;②
為偶函數;②![]() 為偶函數;③
為偶函數;③![]() 的最小值為0;④
的最小值為0;④![]() 有兩個零點.其中真命題的是( ).
有兩個零點.其中真命題的是( ).
A.②④B.①③C.①③④D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在黨中央的正確領導下,通過全國人民的齊心協力,特別是全體一線醫護人員的奮力救治,二月份“新冠肺炎”疫情得到了控制.甲、乙兩個地區采取防護措施后,統計了從2月7日到2月13日一周的新增“新冠肺炎”確診人數,繪制成如下折線圖:
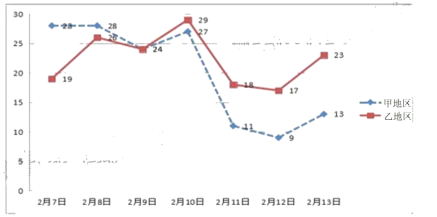
(1)根據圖中甲、乙兩個地區折線圖的信息,寫出你認為最重要的兩個統計結論;
(2)治療“新冠肺炎”藥品的研發成了當務之急,某藥企計劃對甲地區的![]() 項目或乙地區的
項目或乙地區的![]() 項目投入研發資金,經過評估,對于
項目投入研發資金,經過評估,對于![]() 項目,每投資十萬元,一年后利潤是l.38萬元、1.18萬元、l.14萬元的概率分別為
項目,每投資十萬元,一年后利潤是l.38萬元、1.18萬元、l.14萬元的概率分別為![]() 、
、![]() 、
、![]() ;對于
;對于![]() 項目,利潤與產品價格的調整有關,已知
項目,利潤與產品價格的調整有關,已知![]() 項目產品價格在一年內進行2次獨立的調整,每次價格調整中,產品價格下調的概率都是
項目產品價格在一年內進行2次獨立的調整,每次價格調整中,產品價格下調的概率都是![]() ,記
,記![]() 項目一年內產品價格的下調次數為
項目一年內產品價格的下調次數為![]() ,每投資十萬元,
,每投資十萬元,![]() 取0、1、2時,一年后相應利潤是1.4萬元、1.25萬元、0.6萬元.記對
取0、1、2時,一年后相應利潤是1.4萬元、1.25萬元、0.6萬元.記對![]() 項目投資十萬元,一年后利潤的隨機變量為
項目投資十萬元,一年后利潤的隨機變量為![]() ,記對
,記對![]() 項目投資十萬元,一年后利潤的隨機變量為
項目投資十萬元,一年后利潤的隨機變量為![]() .
.
(i)求![]() ,
,![]() 的概率分布列和數學期望
的概率分布列和數學期望![]() ,
,![]() ;
;
(ii)如果你是投資決策者,將做出怎樣的決策?請寫出決策理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() 是橢圓上一動點(與左、右頂點不重合)已知
是橢圓上一動點(與左、右頂點不重合)已知![]() 的內切圓半徑的最大值為
的內切圓半徑的最大值為![]() ,橢圓的離心率為
,橢圓的離心率為![]() .
.
(1)求橢圓C的方程;
(2)過![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,過
兩點,過![]() 作
作![]() 軸的垂線交橢圓
軸的垂線交橢圓![]() 與另一點
與另一點![]() (
(![]() 不與
不與![]() 重合).設
重合).設![]() 的外心為
的外心為![]() ,求證
,求證![]() 為定值.
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com