【題目】四面體
及其三視圖如圖所示，過棱
的中點
作平行于
、
的平面分別交四面體的棱
、
、
于點
、
、
．
（1）求證：四邊形
是矩形；
（2）求點
到面的距離．
【答案】（1）詳見解析（2）
【解析】
（1）由三視圖得到四面體ABCD的具體形狀，然后利用線面平行的性質得到四邊形EFGH的兩組對邊平行，即可得到四邊形為平行四邊形，再由線面垂直的判定和性質得到
，結合異面直線所成角的概念得到
，從而證得結論；
（2）利用線面平行時，直線上的點到平面的距離是相等的，將點
到面
的距離轉化為點D到面的距離，求解即可.
（1）證明：由
,同理可得
所以
由
的面，同理可得
所以
所以四邊形是平行四邊形
由三視圖可知
，所以
,又
所以
,所以四邊形是矩形
（2）易知點到面的距離即
點到面的距離，
由
所以點到面的距離即點到線
的距離
由（1）和
是
的中點可知
、
分別是
、
的中點，
又由三視圖可知
是等腰直角三角形，
易得點到線的距離為，即點到面的距離
心算口算巧算一課一練系列答案科目：高中數學 來源： 題型：
【題目】
，
為空間中兩條互相垂直的直線，等腰直角三角形
的直角邊
所在直線與，都垂直，斜邊
以直線為旋轉軸旋轉，有下列結論：
（1）當直線與成
角時，與成角；
（2）當直線與成
角時，與成角；
（3）直線與所成角的最小值為
；
（4）直線與所成角的最小值為；
其中正確的是______（填寫所有正確結論的編號）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某校甲、乙、丙三個年級的學生志愿者人數分別是240，160，160.現采用分層抽樣的方法從中抽取7名同學去某敬老院參加獻愛心活動。
（1）應從甲、乙、丙三個年級的學生志愿者中分別抽取多少人？
（2）設抽出的7名同學分別用A，B，C，D，E，F，G表示，現從中隨機抽取2名同學承擔敬老院的衛生工作，求事件M“抽取的2名同學來自同一年級”發生的概率。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校為了解高三年級學生寒假期間的學習情況，抽取甲、乙兩班，調查這兩個班的學生在寒假期間每天平均學習的時間（單位：小時），統計結果繪成頻率分別直方圖（如圖）．已知甲、乙兩班學生人數相同，甲班學生每天平均學習時間在區間
的有8人．
（I）求直方圖中
的值及甲班學生每天平均學習時間在區間
的人數；
（II）從甲、乙兩個班每天平均學習時間大于10個小時的學生中任取4人參加測試，設4人中甲班學生的人數為
，求
的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩位學生參加數學競賽培訓．現分別從他們在培訓期間參加的若干次預賽成績中隨機抽取
次．記錄如下：
甲： 
， 
， 
， 
， 
， 
， 
， 
乙： 
， 
， 
， 
， 
， 
， 
， 
（
）用莖葉圖表示這兩組數據．
（
）現要從中選派一人參加數學競賽，從統計學的角度考慮，你認為派哪位學生參加合適?請說明理由．
（
）若將頻率視為概率，對甲同學在今后的三次數學競賽成績進行預測，記這
次成績中高于
分的次數為
，求
的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】學校某研究性學習小組在對學生上課注意力集中情況的調查研究中，發現其在40分鐘的一節課中，注意力指數y與聽課時間x（單位：分鐘）之間的關系滿足如圖所示的圖象，當x∈（0，12]時，圖象是二次函數圖象的一部分，其中頂點A（10，80），過點B（12，78）；當x∈[12，40]時，圖象是線段BC，其中C（40，50）．根據專家研究，當注意力指數大于62時，學習效果最佳．
（1）試求y=f（x）的函數關系式；
（2）教師在什么時段內安排內核心內容，能使得學生學習效果最佳？請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
：
，圓
：
，動圓
與圓外切并且與圓內切，圓心軌跡為曲線
．
（1）求曲線的方程；
（2）若
是曲線上關于
軸對稱的兩點，點
，直線
交曲線
于另一點
，求證：直線
過定點，并求該定點的坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平行六面體ABCD－A1B1C1D1中，AA1⊥平面ABCD，且AB＝AD＝2，AA1＝
，∠BAD＝120°.
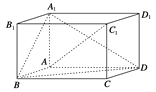
(1)求異面直線A1B與AC1所成角的余弦值；
(2)求二面角B－A1D－A的正弦值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
