
【題目】過雙曲線![]() 的左焦點
的左焦點![]() 作圓
作圓![]() 的切線交雙曲線的右支于點
的切線交雙曲線的右支于點![]() ,且切點為
,且切點為![]() ,已知
,已知![]() 為坐標原點,
為坐標原點,![]() 為線段
為線段![]() 的中點(
的中點(![]() 點在切點
點在切點![]() 的右側),若
的右側),若![]() 的周長為
的周長為![]() ,則雙曲線的漸近線的方程為( )
,則雙曲線的漸近線的方程為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
先從雙曲線方程得:a,b.連OT,則OT⊥F1T,在直角三角形OTF1中,|F1T|=b.連PF2,M為線段F1P的中點,O為坐標原點得出|MO|﹣|MT|![]() PF2﹣(
PF2﹣( ![]() MF1﹣F1T)
MF1﹣F1T)![]() (PF2﹣MF1)﹣b最后結合周長與勾股定理可得結果.
(PF2﹣MF1)﹣b最后結合周長與勾股定理可得結果.
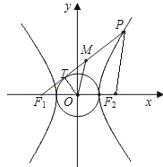
解:連OT,則OT⊥F1T,
在直角三角形OTF1中,|F1T|![]() b.
b.
連PF2,M為線段F1P的中點,O為坐標原點
∴OM![]() PF2,
PF2,
∴|MO|﹣|MT|![]() PF2﹣(
PF2﹣( ![]() PF1﹣F1T)
PF1﹣F1T)![]() (PF2﹣PF1)+b
(PF2﹣PF1)+b
![]() b﹣a.
b﹣a.
又|MO|+|MT|+|TO|=![]() ,即|MO|+|MT|=3a
,即|MO|+|MT|=3a
故|MO|=![]() , |MT|=
, |MT|=![]() ,
,
由勾股定理可得:![]() ,即
,即![]()
∴漸近線方程為:![]()
故選:B


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,從參加環保知識競賽的1200名學生中抽出![]() 名,將其成績(均為整數)整理后畫出的頻率分布直方圖如下:觀察圖形,回答下列問題:
名,將其成績(均為整數)整理后畫出的頻率分布直方圖如下:觀察圖形,回答下列問題:

(1)![]() 這一組的頻數、頻率分別是多少?
這一組的頻數、頻率分別是多少?
(2)估計這次環保知識競賽的及格率。(![]() 分及以上為及格)
分及以上為及格)
(3)若準備取成績最好的300名發獎,則獲獎的最低分數約為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點![]() 為圓
為圓![]() :
:![]() 上一動點,過點
上一動點,過點![]() 分別作
分別作![]() 軸,
軸,![]() 軸的垂線,垂足分別為
軸的垂線,垂足分別為![]() ,
,![]() ,連接
,連接![]() 延長至點
延長至點![]() ,使得
,使得![]() ,點
,點![]() 的軌跡記為曲線
的軌跡記為曲線![]() .
.
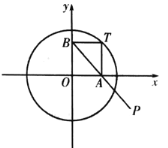
(1)求曲線![]() 的方程;
的方程;
(2)若點![]() ,
,![]() 分別位于
分別位于![]() 軸與
軸與![]() 軸的正半軸上,直線
軸的正半軸上,直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,試問在曲線
兩點,試問在曲線![]() 上是否存在點
上是否存在點![]() ,使得四邊形
,使得四邊形![]() 為平行四邊形,若存在,求出直線
為平行四邊形,若存在,求出直線![]() 方程;若不存在,說明理由.
方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】市面上有某品牌![]() 型和
型和![]() 型兩種節能燈,假定
型兩種節能燈,假定![]() 型節能燈使用壽命都超過5000小時,經銷商對
型節能燈使用壽命都超過5000小時,經銷商對![]() 型節能燈使用壽命進行了調查統計,得到如下頻率分布直方圖:
型節能燈使用壽命進行了調查統計,得到如下頻率分布直方圖:

某商家因原店面需要重新裝修,需租賃一家新店面進行周轉,合約期一年.新店面需安裝該品牌節能燈5支(同種型號)即可正常營業.經了解,![]() 型20瓦和
型20瓦和![]() 型55瓦的兩種節能燈照明效果相當,都適合安裝.已知
型55瓦的兩種節能燈照明效果相當,都適合安裝.已知![]() 型和
型和![]() 型節能燈每支的價格分別為120元、25元,當地商業電價為0.75元/千瓦時.假定該店面一年周轉期的照明時間為3600小時,若正常營業期間燈壞了立即購買同型燈管更換.(用頻率估計概率)
型節能燈每支的價格分別為120元、25元,當地商業電價為0.75元/千瓦時.假定該店面一年周轉期的照明時間為3600小時,若正常營業期間燈壞了立即購買同型燈管更換.(用頻率估計概率)
(Ⅰ)根據頻率直方圖估算![]() 型節能燈的平均使用壽命;
型節能燈的平均使用壽命;
(Ⅱ)根據統計知識知,若一支燈管一年內需要更換的概率為![]() ,那么
,那么![]() 支燈管估計需要更換
支燈管估計需要更換![]() 支.若該商家新店面全部安裝了
支.若該商家新店面全部安裝了![]() 型節能燈,試估計一年內需更換的支數;
型節能燈,試估計一年內需更換的支數;
(Ⅲ)若只考慮燈的成本和消耗電費,你認為該商家應選擇哪種型號的節能燈,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
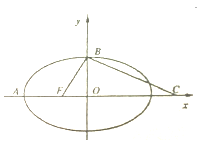
【題目】如圖,F是橢圓![]() 的左焦點,橢圓的離心率為
的左焦點,橢圓的離心率為![]() ,B為橢圓的左頂點和上頂點,點C在x軸上,
,B為橢圓的左頂點和上頂點,點C在x軸上,![]() ,
,![]() 的外接圓M恰好與直線
的外接圓M恰好與直線![]() :
:![]() 相切.
相切.
![]() 1
1![]() 求橢圓的方程;
求橢圓的方程;
![]() 2
2![]() 過點C的直線
過點C的直線![]() 與已知橢圓交于P,Q兩點,且
與已知橢圓交于P,Q兩點,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱長為![]() 的正方體
的正方體![]() 中,
中,![]() ,
,![]() ,
,![]() 分別是棱
分別是棱![]() 、
、![]() 和
和![]() 所在直線上的動點:
所在直線上的動點:

(1)求![]() 的取值范圍:
的取值范圍:
(2)若![]() 為面
為面![]() 內的一點,且
內的一點,且![]() ,
,![]() ,求
,求![]() 的余弦值:
的余弦值:
(3)若![]() 、
、![]() 分別是所在正方形棱的中點,試問在棱
分別是所在正方形棱的中點,試問在棱![]() 上能否找到一點
上能否找到一點![]() ,使
,使![]() 平面
平面![]() ?若能,試確定點
?若能,試確定點![]() 的位置,若不能,請說明理由.
的位置,若不能,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國西部某省![]() 級風景區內住著一個少數民族村,該村投資了
級風景區內住著一個少數民族村,該村投資了![]() 萬元修復和加強民俗文化基礎設施,據調查,修復好村民俗文化基礎設施后,任何一個月內(每月按
萬元修復和加強民俗文化基礎設施,據調查,修復好村民俗文化基礎設施后,任何一個月內(每月按![]() 天計算)每天的旅游人數
天計算)每天的旅游人數![]() 與第
與第![]() 天近似地滿足
天近似地滿足![]() (千人),且參觀民俗文化村的游客人均消費
(千人),且參觀民俗文化村的游客人均消費![]() 近似地滿足
近似地滿足![]() (元).
(元).
(1)求該村的第x天的旅游收入![]() ,并求最低日收入為多少?(單位:千元,
,并求最低日收入為多少?(單位:千元,![]() ,
,![]() );
);
(2)若以最低日收入的![]() 作為每一天的純收入計量依據,并以純收入的
作為每一天的純收入計量依據,并以純收入的![]() 稅率收回投資成本,試問該村在兩年內能否收回全部投資成本?
稅率收回投資成本,試問該村在兩年內能否收回全部投資成本?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com