
【題目】已知函數f(x)是奇函數,且滿足f(2﹣x)=f(x)(x∈R),當0<x≤1時,f(x)=lnx+2,則函數y=f(x)在(﹣2,4]上的零點個數是( )
A.7
B.8
C.9
D.10
【答案】C
【解析】解:由函數f(x)是奇函數且滿足f(2﹣x)=f(x)知,f(x)是周期為4的周期函數, 且關于直線x=1+2k(k∈R)成軸對稱,關于點(2k,0)(k∈Z)成中心對稱.
當0<x≤1時,令f(x)=lnx+2=0,得 ![]() ,由此得y=f(x)在(﹣2,4]上的零點分別為
,由此得y=f(x)在(﹣2,4]上的零點分別為 ![]() ,
, ![]() ,0,
,0, ![]() ,
, ![]() ,2,
,2, ![]() ,
, ![]() ,4共9個零點.
,4共9個零點.
故選C.
【考點精析】本題主要考查了函數奇偶性的性質的相關知識點,需要掌握在公共定義域內,偶函數的加減乘除仍為偶函數;奇函數的加減仍為奇函數;奇數個奇函數的乘除認為奇函數;偶數個奇函數的乘除為偶函數;一奇一偶的乘積是奇函數;復合函數的奇偶性:一個為偶就為偶,兩個為奇才為奇才能正確解答此題.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】四棱錐P﹣ABCD中,底面ABCD為矩形, ![]() 為BC的中點,連接AE,BD,交點H,PH⊥平面ABCD,M為PD的中點.
為BC的中點,連接AE,BD,交點H,PH⊥平面ABCD,M為PD的中點. 
(1)求證:平面MAE⊥平面PBD;
(2)設PE=1,求二面角M﹣AE﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知正四棱錐P﹣ABCD中,PA=AB=2,點M,N分別在PA,BD上,且 ![]() =
= ![]() .
. 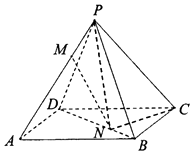
(1)求異面直線MN與PC所成角的大小;
(2)求二面角N﹣PC﹣B的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知右焦點為F2(c,0)的橢圓C: ![]() +
+ ![]() =1(a>b>0)過點(1,
=1(a>b>0)過點(1, ![]() ),且橢圓C關于直線x=c對稱的圖形過坐標原點.
),且橢圓C關于直線x=c對稱的圖形過坐標原點.
(1)求橢圓C的方程;
(2)過點( ![]() ,0)作直線l與橢圓C交于E,F兩點,線段EF的中點為M,點A是橢圓C的右頂點,求直線MA的斜率k的取值范圍.
,0)作直線l與橢圓C交于E,F兩點,線段EF的中點為M,點A是橢圓C的右頂點,求直線MA的斜率k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為創建全國文明城市,某區向各事業行政單位征集“文明過馬路”義務督導員.從符合條件的600名志愿者中隨機抽取100名,按年齡作分組如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下頻率分布直方圖.
(Ⅰ)求圖中x的值,并根據頻率分布直方圖統計這600名志愿者中年齡在[30.40)的人數;
(Ⅱ)在抽取的100名志愿者中按年齡分層抽取10名參加區電視臺“文明伴你行”節目錄制,再從這10名志愿者中隨機選取3名到現場分享勸導制止行人闖紅燈的經歷,記這3名志愿者中年齡不低于35歲的人數為X,求X的分布列及數學期望.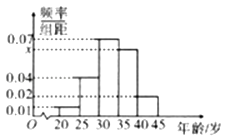
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題正確是 , (寫出所有正確命題的序號)
①若奇函數f(x)的周期為4,則函數f(x)的圖象關于(2,0)對稱;
②若a∈(0,1),則a1+a<a ![]() ;
;
③函數f(x)=ln ![]() 是奇函數;
是奇函數;
④存在唯一的實數a使f(x)=lg(ax+ ![]() )為奇函數.
)為奇函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線的頂點在坐標原點,焦點F在y軸正半軸上,過點F的直線交拋物線于A,B兩點,線段AB的長是8,AB的中點到x軸的距離是3.
(1)求拋物線的標準方程;
(2)設直線m在y軸上的截距為6,且與拋物線交于P,Q兩點,連結QF并延長交拋物線的準線于點R,當直線PR恰與拋物線相切時,求直線m的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)的表達式為f(x)= ![]() (c≠0),則函數f(x)的圖象的對稱中心為(﹣
(c≠0),則函數f(x)的圖象的對稱中心為(﹣ ![]() ,
, ![]() ),現已知函數f(x)=
),現已知函數f(x)= ![]() ,數列{an}的通項公式為an=f(
,數列{an}的通項公式為an=f( ![]() )(n∈N),則此數列前2017項的和為 .
)(n∈N),則此數列前2017項的和為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com