
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,
, ![]() 是橢圓
是橢圓![]() 上任意一點,且點
上任意一點,且點![]() 到橢圓
到橢圓![]() 的一個焦點的最大距離等于
的一個焦點的最大距離等于![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若過點![]() 的直線與橢圓
的直線與橢圓![]() 相交于不同兩點
相交于不同兩點![]() ,設
,設![]() 為橢圓上一點,是否存在整數
為橢圓上一點,是否存在整數![]() ,使得
,使得![]() (其中
(其中![]() 為坐標原點)?若存在,試求整數
為坐標原點)?若存在,試求整數![]() 的所有取值;若不存在,請說明理由.
的所有取值;若不存在,請說明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)整數
;(Ⅱ)整數![]() 的所有取值為-1,0,1.
的所有取值為-1,0,1.
【解析】試題分析:(Ⅰ)由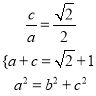 ,解得
,解得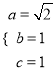 ,則橢圓方程可求;
,則橢圓方程可求;
(Ⅱ)設出直線方程,和橢圓聯立后化為關于![]() 的一元二次方程,由判別式大于
的一元二次方程,由判別式大于![]() 求出
求出![]() 的范圍,利用根與系數關系得到
的范圍,利用根與系數關系得到![]() 兩點的橫坐標的和與積,代入
兩點的橫坐標的和與積,代入![]() 后得到
后得到![]() 點的坐標,把
點的坐標,把![]() 點坐標代入橢圓方程后得到
點坐標代入橢圓方程后得到![]() 與
與![]() 的關系,由
的關系,由![]() 的范圍確定
的范圍確定![]() 的范圍.
的范圍.
試題解析:(Ⅰ)設橢圓![]() 的半焦距為
的半焦距為![]() ,則由題意知
,則由題意知
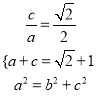 ,解得
,解得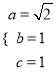 ,
,
所以橢圓![]() 的方程為
的方程為![]() .
.
(Ⅱ)結論:存在整數![]() ,使得
,使得![]() .理由如下:
.理由如下:
由題意知直線![]() 的斜率存在.
的斜率存在.
設![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
由方程組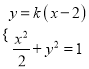 ,消去
,消去![]() 整理得
整理得![]() .
.
∵直線![]() 與橢圓
與橢圓![]() 有兩個不同的公共點,
有兩個不同的公共點,
∴![]()
![]() ,解得
,解得![]() .
.
而![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴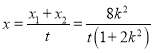 ,
, ![]()
![]()
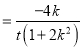 .
.
∵點![]() 在橢圓上,∴
在橢圓上,∴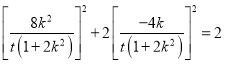 ,
,
∴![]()
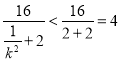 ,即
,即![]() ,解得
,解得![]() ,
,
∴整數![]() 的所有取值為-1,0,1.
的所有取值為-1,0,1.


科目:高中數學 來源: 題型:
【題目】已知函數/ ![]() (
(![]() 為常數)的圖像與
為常數)的圖像與![]() 軸交于點
軸交于點![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線斜率為
處的切線斜率為![]() .
.
(1)求![]() 的值及函數的極值;
的值及函數的極值;
(2)證明:當![]() 時,
時, ![]() ;
;
(3)證明:對任意給定的正數![]() ,總存在
,總存在![]() ,使得當
,使得當![]() ,恒有
,恒有![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2015年8月12日天津發生危化品重大爆炸事故,造成重大人員和經濟損失.某港口組織消防人員對該港口的公司的集裝箱進行安全抽檢,已知消防安全等級共分為四個等級(一級為優,二級為良,三級為中等,四級為差),該港口消防安全等級的統計結果如下表所示:

現從該港口隨機抽取了![]() 家公司,其中消防安全等級為三級的恰有20家.
家公司,其中消防安全等級為三級的恰有20家.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)按消防安全等級利用分層抽樣的方法從這![]() 家公司中抽取10家,除去消防安全等級為一級和四級的公司后,再從剩余公司中任意抽取2家,求抽取的這2家公司的消防安全等級都是二級的概率.
家公司中抽取10家,除去消防安全等級為一級和四級的公司后,再從剩余公司中任意抽取2家,求抽取的這2家公司的消防安全等級都是二級的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠生產某種產品的月固定成本為10(萬元),每生產![]() 件,需另投入成本為
件,需另投入成本為![]() (萬元).當月產量不足30件時,
(萬元).當月產量不足30件時, ![]() (萬元);當月產量不低于30件時,
(萬元);當月產量不低于30件時, ![]() (萬元).因設備問題,該廠月生產量不超過50件.現已知此商品每件售價為5萬元,且該廠每個月生產的商品都能當月全部銷售完.
(萬元).因設備問題,該廠月生產量不超過50件.現已知此商品每件售價為5萬元,且該廠每個月生產的商品都能當月全部銷售完.
(1)寫出月利潤![]() (萬元)關于月產量
(萬元)關于月產量![]() (件)的函數解析式;
(件)的函數解析式;
(2)當月產量為多少件時,該廠所獲月利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別是a,b,c已知ccosB+(b-2a)cosC=0
(1)求角C的大小
(2)若c=2,a+b=ab,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司利用簡單隨機抽樣方法,對投保車輛進行抽樣,樣本車輛中每輛車的賠付結果統計如下:
賠付金額(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
車輛數(輛) | 500 | 130 | 100 | 150 | 120 |
(1)若每輛車的投保金額均為2800元,估計賠付金額大于投保金額的概率.
(2)在樣本車輛中,車主是新司機的占10%,在賠付金額為4000元的樣本車輛中,車主是新司機的占20%,估計在已投保車輛中,新司機獲賠金額為4000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為做好2022年北京冬季奧運會的宣傳工作,組委會計劃從某大學選取若干大學生志愿者,某記者在該大學隨機調查了1000名大學生,以了解他們是否愿意做志愿者工作,得到的數據如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合計 | |
男大學生 | 610 | ||
女大學生 | 90 | ||
合計 | 800 |
(1) 根據題意完成表格;
(2) 是否有![]() 的把握認為愿意做志愿者工作與性別有關?
的把握認為愿意做志愿者工作與性別有關?
參考公式及數據: 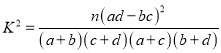 ,其中
,其中![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某智能手機制作完成之后還需要依次通過三道嚴格的審核程序,已知第一道審核、第二道審核、第三道審核通過的概率分別為![]() ,每道程序是相互獨立的,且一旦審核不通過就停止審核,每部手機只有三道程序都通過才能出廠銷售.
,每道程序是相互獨立的,且一旦審核不通過就停止審核,每部手機只有三道程序都通過才能出廠銷售.
(1)求審核過程中只進行兩道程序就停止審核的概率;
(2)現有3部該智能手機進入審核,記這3部手機可以出廠銷售的部數為![]() ,求X的分布列及數學期望.
,求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設橢圓![]() :
: ![]() ,長軸的右端點與拋物線
,長軸的右端點與拋物線![]() :
: ![]() 的焦點
的焦點![]() 重合,且橢圓
重合,且橢圓![]() 的離心率是
的離心率是![]() .
.
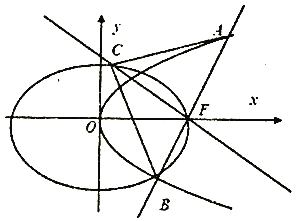
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過![]() 作直線
作直線![]() 交拋物線
交拋物線![]() 于
于![]() ,
, ![]() 兩點,過
兩點,過![]() 且與直線
且與直線![]() 垂直的直線交橢圓
垂直的直線交橢圓![]() 于另一點
于另一點![]() ,求
,求![]() 面積的最小值,以及取到最小值時直線
面積的最小值,以及取到最小值時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com