
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為直角梯形,
為直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() ,
, ![]() 是棱
是棱![]() 上的點.
上的點.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() ,
, ![]() ,異面直線
,異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() ,求
,求![]() 的值.
的值.

【答案】(1)見解析;(2)![]() 或
或![]()
【解析】試題分析:(1)根據![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,推出四邊形
的中點,推出四邊形![]() 為平行四邊形,再由
為平行四邊形,再由![]() ,推出
,推出![]() ,結合平面
,結合平面![]() 平面
平面![]() ,即可證
,即可證![]() 平面
平面![]() ,從而得證平面
,從而得證平面![]() 平面
平面![]() ;(2)根據題設條件易證
;(2)根據題設條件易證![]() 平面
平面![]() ,以
,以![]() 為原點分別以
為原點分別以![]() 、
、![]() 、
、![]() 為
為![]() 軸、
軸、![]() 軸、
軸、![]() 軸的正方向建立空間直角坐標系,設
軸的正方向建立空間直角坐標系,設![]() ,
, ![]() ,化簡可得
,化簡可得![]() ,再根據異面直線
,再根據異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() ,列出方程,解得即可得出
,列出方程,解得即可得出![]() 的值.
的值.
試題解析:(1)證明:∵![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,
的中點,
∴四邊形![]() 為平行四邊形
為平行四邊形
∴![]() .
.
∵![]()
∴![]() ,即
,即![]() .
.
又∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() .
.
∴![]() 平面
平面![]()
∵![]() 平面
平面![]()
∴平面![]() 平面
平面![]() .
.
(2)∵![]() ,
, ![]() 為
為![]() 的中點
的中點
∴![]() .
.
∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() .
.
以![]() 為原點分別以
為原點分別以![]() 、
、![]() 、
、![]() 為
為![]() 軸、
軸、![]() 軸、
軸、![]() 軸的正方向建立空間直角坐標系,則
軸的正方向建立空間直角坐標系,則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,設
,設![]() .
.
∴![]() ,
, ![]() ,
, ![]() .
.
由![]() 是
是![]() 上的點,設
上的點,設![]() ,化簡得
,化簡得![]() .
.
設異面直線![]() 與
與![]() 所成角為
所成角為![]() ,則
,則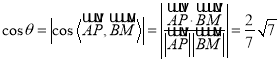 .
.
∴![]() ,計算得
,計算得![]() 或
或![]() ,故
,故![]() 或
或![]() .
.


科目:高中數學 來源: 題型:
【題目】下表數據為某地區某種農產品的年產量x(單位:噸)及對應銷售價格y(單位:千元/噸) .
x | 1 | 2 | 3 | 4 | 5 |
y | 70 | 65 | 55 | 38 | 22 |
(1)若y與x有較強的線性相關關系,根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程.
(2)若該農產品每噸的成本為13.1千元,假設該農產品可全部賣出,利用上問所求的回歸方程,預測當年產量為多少噸時,年利潤Z最大?
(參考公式:回歸直線方程為![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數![]() 有下述四個結論:①若
有下述四個結論:①若![]() ,則
,則![]() ;②
;②![]() 的圖象關于點
的圖象關于點![]() 對稱;③函數
對稱;③函數![]() 在
在![]() 上單調遞增;④
上單調遞增;④![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后所得圖象關于
個單位長度后所得圖象關于![]() 軸對稱.其中所有正確結論的編號是( )
軸對稱.其中所有正確結論的編號是( )
A.①②④B.①②C.③④D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間租賃甲、乙兩種設備生產A,B兩類產品,甲種設備每天能生產A類產品8件和B類產品15件,乙種設備每天能生產A類產品10件和B類產品25件,已知設備甲每天的租賃費300元,設備乙每天的租賃費400元,現車間至少要生產A類產品100件,B類產品200件,所需租賃費最少為__元![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,已知曲線![]() ,將曲線
,將曲線![]() 上的點向左平移一個單位,然后縱坐標不變,橫坐標軸伸長到原來的2倍,得到曲線
上的點向左平移一個單位,然后縱坐標不變,橫坐標軸伸長到原來的2倍,得到曲線![]() ,又已知直線
,又已知直線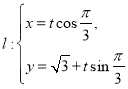 (
(![]() 是參數),且直線
是參數),且直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點.
兩點.
(I)求曲線![]() 的直角坐標方程,并說明它是什么曲線;
的直角坐標方程,并說明它是什么曲線;
(II)設定點![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區高考實行新方案,規定:語文、數學和英語是考生的必考科目,考生還須從物理、化學、生物、歷史、地理和政治六個科目中選取三個科目作為選考科目.若一個學生從六個科目中選出了三個科目作為選考科目,則稱該學生的選考方案確定;否則,稱該學生選考方案待確定.例如,學生甲選擇“物理、化學和生物”三個選考科目,則學生甲的選考方案確定,“物理、化學和生物”為其選考方案.
某學校為了解高一年級420名學生選考科目的意向,隨機選取30名學生進行了一次調查,統計選考科目人數如下表: