
【題目】已知函數(shù)f(x)= ![]() .
.
(1)證明函數(shù)f(x)在(﹣1,+∞)上為單調(diào)遞增函數(shù);
(2)若x∈[0,2],求函數(shù)f(x)的值域.
【答案】
(1)證法一: ![]() .
.
設(shè)x1,x2是區(qū)間(﹣1,+∞)上的兩個任意實數(shù),且x1<x2,
于是 ![]() =
= ![]() .
.
因為x2>x1>﹣1,所以x1+1>0,x2+1>0,x2﹣x1>0,
所以f(x2)﹣f(x1)>0,所以f(x1)<f(x2),
所以函數(shù)f(x)在(﹣1,+∞)上為單調(diào)增函數(shù).
證法二:∵f(x)= ![]() .
.
∴f′(x)= ![]() .
.
當(dāng)x∈(﹣1,+∞)時,
f′(x)>0恒成立,
故函數(shù)f(x)在(﹣1,+∞)上為單調(diào)遞增函數(shù)
(2)解:由(1)可知,函數(shù)在[0,2]上為單調(diào)增函數(shù),
于是,當(dāng)x∈[0,2]時,f(x)min=f(0)=1,…(11分) ![]() .
.
所以,當(dāng)x∈[0,2]時,函數(shù)f(x)的值域為 ![]()
【解析】(1)證法一:設(shè)x1 , x2是區(qū)間(﹣1,+∞)上的兩個任意實數(shù),且x1<x2 , 作差判斷f(x1),f(x2)的大小,可得緒論
證法二:求導(dǎo),根據(jù)x∈(﹣1,+∞)時,f′(x)>0恒成立,可得:函數(shù)f(x)在(﹣1,+∞)上為單調(diào)遞增函數(shù);(2)根據(jù)(1)中函數(shù)的單調(diào)性,求出函數(shù)的最值,進而可得函數(shù)的值域.
【考點精析】解答此題的關(guān)鍵在于理解函數(shù)的值域的相關(guān)知識,掌握求函數(shù)值域的方法和求函數(shù)最值的常用方法基本上是相同的.事實上,如果在函數(shù)的值域中存在一個最小(大)數(shù),這個數(shù)就是函數(shù)的最小(大)值.因此求函數(shù)的最值與值域,其實質(zhì)是相同的,以及對函數(shù)單調(diào)性的判斷方法的理解,了解單調(diào)性的判定法:①設(shè)x1,x2是所研究區(qū)間內(nèi)任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,已知3acosA=ccosB+bcosC.
(1)求cosA,sinA的值;
(2)若cosB+cosC= ![]() ,求cosC+
,求cosC+ ![]() sinC的值.
sinC的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,已知C= ![]() ,向量
,向量 ![]() =(sinA,1),
=(sinA,1), ![]() =(1,cosB),且
=(1,cosB),且 ![]() .
.
(1)求A的值;
(2)若點D在邊BC上,且3 ![]() =
= ![]() ,
, ![]() =
= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)p:實數(shù)x滿足x2﹣4ax+3a2<0,其中a>0; q:實數(shù)x滿足 ![]() <0.
<0.
(1)若a=1,且p∨q為真,求實數(shù)x的取值范圍;
(2)若p是q的必要不充分條件,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,有一塊矩形空地ABCD,AB=2km,BC=4km,根據(jù)周邊環(huán)境及地形實際,當(dāng)?shù)卣?guī)劃在該空地內(nèi)建一個箏形商業(yè)區(qū)AEFG,箏形的頂點A,E,F(xiàn),G為商業(yè)區(qū)的四個入口,其中入口F在邊BC上(不包含頂點),入口E,G分別在邊AB,AD上,且滿足點A,F(xiàn)恰好關(guān)于直線EG對稱,矩形內(nèi)箏形外的區(qū)域均為綠化區(qū). 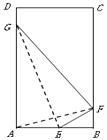
(1)請確定入口F的選址范圍;
(2)設(shè)商業(yè)區(qū)的面積為S1 , 綠化區(qū)的面積為S2 , 商業(yè)區(qū)的環(huán)境舒適度指數(shù)為 ![]() ,則入口F如何選址可使得該商業(yè)區(qū)的環(huán)境舒適度指數(shù)最大?
,則入口F如何選址可使得該商業(yè)區(qū)的環(huán)境舒適度指數(shù)最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過點![]() 作曲線
作曲線![]() (其中
(其中![]() 為自然對數(shù)的底數(shù))的切線,切點為
為自然對數(shù)的底數(shù))的切線,切點為![]() ,設(shè)
,設(shè)![]() 在
在![]() 軸上的投影是點
軸上的投影是點![]() ,過點
,過點![]() 再作曲線
再作曲線![]() 的切線,切點為
的切線,切點為![]() ,設(shè)
,設(shè)![]() 在
在![]() 軸上的投影是點
軸上的投影是點![]() ,依次下去,得到第
,依次下去,得到第![]() 個切點
個切點![]() ,則點
,則點![]() 的坐標(biāo)為________.
的坐標(biāo)為________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,已知橢圓
中,已知橢圓![]() 的左右頂點為
的左右頂點為![]() ,右焦點為
,右焦點為![]() ,一條準(zhǔn)線方程是
,一條準(zhǔn)線方程是![]() ,點
,點![]() 為橢圓
為橢圓![]() 上異于
上異于![]() 的兩點,點
的兩點,點![]() 為
為![]() 的中點.
的中點.
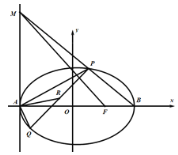
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)直線![]() 交直線
交直線![]() 于點
于點![]() ,記直線
,記直線![]() 的斜率為
的斜率為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,求證:
,求證:![]() 為定值;
為定值;
(3)若![]() ,求直線
,求直線![]() 斜率的取值范圍。
斜率的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我國古代數(shù)學(xué)著作《九章算術(shù)》有如下問題:“今有人持金出五關(guān),前關(guān)二而稅一,次關(guān)三而稅一,次關(guān)四而稅一,次關(guān)五而稅一,次關(guān)六而稅一,并五關(guān)所稅,適重一斤,問本持金幾何”其意思為“今有人持金出五關(guān),第1關(guān)收稅金 ![]() ,第2關(guān)收稅金為剩余金的
,第2關(guān)收稅金為剩余金的 ![]() ,第3關(guān)收稅金為剩余金的
,第3關(guān)收稅金為剩余金的 ![]() ,第4關(guān)收稅金為剩余金的
,第4關(guān)收稅金為剩余金的 ![]() ,第5關(guān)收稅金為剩余金的
,第5關(guān)收稅金為剩余金的 ![]() ,5關(guān)所收稅金之和,恰好重1斤,問原來持金多少?”若將題中“5關(guān)所收稅金之和,恰好重1斤,問原來持金多少?”改成假設(shè)這個原來持金為x,按此規(guī)律通過第8關(guān),則第8關(guān)需收稅金為x.
,5關(guān)所收稅金之和,恰好重1斤,問原來持金多少?”若將題中“5關(guān)所收稅金之和,恰好重1斤,問原來持金多少?”改成假設(shè)這個原來持金為x,按此規(guī)律通過第8關(guān),則第8關(guān)需收稅金為x.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)= ![]() ,若曲線f(x)在點(e,f(e))處的切線與直線e2x﹣y+e=0垂直(其中e為自然對數(shù)的底數(shù)).
,若曲線f(x)在點(e,f(e))處的切線與直線e2x﹣y+e=0垂直(其中e為自然對數(shù)的底數(shù)).
(1)若f(x)在(m,m+1)上存在極值,求實數(shù)m的取值范圍;
(2)求證:當(dāng)x>1時, ![]() >
> ![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com