
【題目】對于數(shù)列![]() :
:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,若不改變
,若不改變![]() ,僅改變
,僅改變![]() 、
、![]() 、
、![]() 、
、![]() 中部分項的符號(可以都不改變),得到的新數(shù)列
中部分項的符號(可以都不改變),得到的新數(shù)列![]() 稱為數(shù)列
稱為數(shù)列![]() 的一個生成數(shù)列,如僅改變數(shù)列
的一個生成數(shù)列,如僅改變數(shù)列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的第二、三項的符號,可以得到一個生成數(shù)列:
的第二、三項的符號,可以得到一個生成數(shù)列:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .已知數(shù)列
.已知數(shù)列![]() 為數(shù)列
為數(shù)列![]() 的生成數(shù)列,
的生成數(shù)列,![]() 為數(shù)列
為數(shù)列![]() 的前
的前![]() 項和.
項和.
(1)寫出![]() 的所有可能的值;
的所有可能的值;
(2)若生成數(shù)列![]() 的通項公式為
的通項公式為 ,求
,求![]() ;
;
(3)用數(shù)學(xué)歸納法證明:對于給定的![]() ,
,![]() 的所有可能值組成的集合為
的所有可能值組成的集合為![]() .
.
【答案】(1)![]() 、
、![]() 、
、![]() 、
、![]() ;(2)
;(2)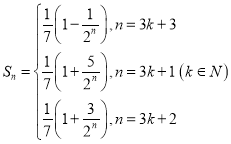 ;(3)證明見解析.
;(3)證明見解析.
【解析】
(1)根據(jù)生成數(shù)列定義,可知當(dāng)![]() 時,
時,![]() ,
,![]() 、
、![]() 分別為
分別為![]() 、
、![]() 中取值,由此給出
中取值,由此給出![]() 的所有可能的情況,即可計算出
的所有可能的情況,即可計算出![]() 的所有可能值;
的所有可能值;
(2)利用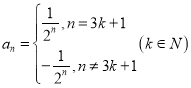 ,分
,分![]() 、
、![]() 、
、![]() 三種情況討論,利用分組求和與等比數(shù)列的求和公式即可求得
三種情況討論,利用分組求和與等比數(shù)列的求和公式即可求得![]() ;
;
(3)利用數(shù)學(xué)歸納法證明:①當(dāng)![]() 時命題成立;②假設(shè)當(dāng)
時命題成立;②假設(shè)當(dāng)![]() 時,
時,![]() ,證明出
,證明出![]() ,結(jié)合歸納原理即可證明出結(jié)論成立.
,結(jié)合歸納原理即可證明出結(jié)論成立.
(1)由題意得![]() ,
,![]() ,
,
根據(jù)生成數(shù)列的定義,可得![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,
因此,![]() 所有可能的取值為
所有可能的取值為![]() 、
、![]() 、
、![]() 、
、![]() ;
;
(2)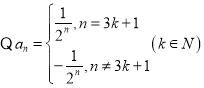 ,
,
當(dāng)![]() 時,
時,![]()
![]()
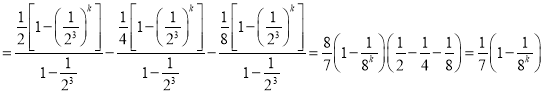
![]() ;
;
當(dāng)![]() 時,
時,![]() ;
;
當(dāng)![]() 時,
時,![]() .
.
綜上所述: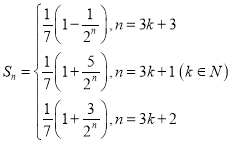 ;
;
(3)利用數(shù)學(xué)歸納法證明:
①當(dāng)![]() 時,
時,![]() ,命題成立;
,命題成立;
②假設(shè)當(dāng)![]() 時,命題成立,即
時,命題成立,即![]() 所有可能值的集合為
所有可能值的集合為![]() .
.
由假設(shè)得![]() .
.
則當(dāng)![]() 時,
時,![]()
![]() .
.
即![]() 或
或![]() ,
,
即![]() ,
,
![]() 當(dāng)
當(dāng)![]() 時,命題成立.
時,命題成立.
由①②知,對于給定的![]() ,
,![]() 的所有可能值組成的集合為
的所有可能值組成的集合為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了研究某藥品的療效,選取若干名志愿者進(jìn)行臨床試驗,所有志愿者的舒張壓數(shù)據(jù)(單位:kPa)的分組區(qū)間為[12,13),[13,14),[14,15),[15,16),[16,17],將其按從左到右的順序分別編號為第一組,第二組,![]() ,第五組,右圖是根據(jù)試驗數(shù)據(jù)制成的頻率分布直方圖,已知第一組與第二組共有20人,第三組中沒有療效的有6人,則第三組中有療效的人數(shù)為( )
,第五組,右圖是根據(jù)試驗數(shù)據(jù)制成的頻率分布直方圖,已知第一組與第二組共有20人,第三組中沒有療效的有6人,則第三組中有療效的人數(shù)為( )
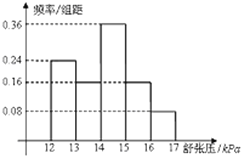
A. 6 B. 8 C. 12 D. 18
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于以下四個命題:①兩條異面直線有無數(shù)條公垂線;②直線在平面內(nèi)的射影是直線;③如果兩條直線在同一個平面內(nèi)的射影平行,那這兩條直線平行;④過兩條異面直線的一條有且僅有一個平面與已知直線平行;上述命題中為真命題的個數(shù)為( )個
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() :
:![]() 的焦點為
的焦點為![]() ,其準(zhǔn)線
,其準(zhǔn)線![]() :
:![]() 與
與![]() 軸的交點為
軸的交點為![]() ,過點
,過點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點.
兩點.
(1)求拋物線![]() 的方程;
的方程;
(2)點![]() 關(guān)于
關(guān)于![]() 軸的對稱點為
軸的對稱點為![]() ,證明:存在實數(shù)
,證明:存在實數(shù)![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在![]() 中,已知
中,已知![]() 、
、![]() .
.
(1)若點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,直線
,直線![]() ,直線
,直線![]() 交
交![]() 邊于
邊于![]() ,交
,交![]() 邊于
邊于![]() ,且
,且![]() 與
與![]() 的面積之比為
的面積之比為![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)若![]() 是一個動點,且
是一個動點,且![]() 的面積為
的面積為![]() ,試求
,試求![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式.
的函數(shù)關(guān)系式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一次足球邀請賽共安排了![]() 支球隊參加,每支球隊預(yù)定的比賽場數(shù)分別是
支球隊參加,每支球隊預(yù)定的比賽場數(shù)分別是![]() ,
,![]() ,…,
,…,![]() .若任兩支球隊之間至多安排了一場比賽,則稱
.若任兩支球隊之間至多安排了一場比賽,則稱![]() 是一個“有效安排”.證明:若
是一個“有效安排”.證明:若![]() 是一個有效安排,且
是一個有效安排,且![]() ,則可去掉一支球隊,并重新調(diào)整各隊之間的對局情況,使
,則可去掉一支球隊,并重新調(diào)整各隊之間的對局情況,使![]() 也是一個有效安排.
也是一個有效安排.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com