【題目】已知直三棱柱
中的底面為等腰直角三角形，
，點
分別是邊
，
上動點，若直線
平面
，點
為線段
的中點，則點的軌跡為
A. 雙曲線的一支一部分 B. 圓弧一部分
C. 線段去掉一個端點 D. 拋物線的一部分
每日10分鐘口算心算速算天天練系列答案科目：高中數學 來源： 題型：
【題目】已知函數
的最大值為
，其圖像相鄰的兩條對稱軸之間的距離為
，且
的圖像關于點
對稱，則下列結論正確的是（ ）.
A.函數的圖像關于直線
對稱
B.當
時，函數的最小值為
C.若
，則
的值為
D.要得到函數的圖像，只需要將
的圖像向右平移
個單位
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2018年茂名市舉辦“好心杯”少年美術書法作品比賽，某賽區收到200件參賽作品，為了解作品質量，現從這些作品中隨機抽取12件作品進行試評.成績如下：67,82,78,86,96,81,73,84,76,59,85,93.
（1）求該樣本的中位數和方差；
（2）若把成績不低于85分（含85分）的作品認為為優秀作品，現在從這12件作品中任意抽取3件，求抽到優秀作品的件數的分布列和期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某調查機構對某校學生做了一個是否同意生“二孩”抽樣調查，該調查機構從該校隨機抽查了100名不同性別的學生，調查統計他們是同意父母生“二孩”還是反對父母生“二孩”，現已得知100人中同意父母生“二孩”占60%，統計情況如下表：
同意 | 不同意 | 合計 | |
男生 | a | 5 | |
女生 | 40 | d | |
合計 | 100 |
（1）求 a，d 的值，根據以上數據，能否有97.5%的把握認為是否同意父母生“二孩”與性別有關?請說明理由；
（2）將上述調查所得的頻率視為概率，現在從所有學生中，采用隨機抽樣的方法抽取4 位學生進行長期跟蹤調查，記被抽取的4位學生中持“同意”態度的人數為 X，求 X 的分布列及數學期望.
附：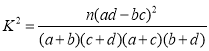
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目：高中數學 來源： 題型：
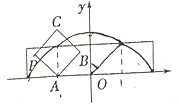
【題目】如圖放置的邊長為1的正方形
沿
軸滾動，點
恰好經過原點.設頂點
的軌跡方程是
，則對函數有下列判斷：①函數是偶函數；②對任意的
，都有
；③函數在區間
上單調遞減；④函數的值域是
；⑤
.其中判斷正確的序號是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在2016年8月巴西里約熱內盧舉辦的第31屆奧運會上，乒乓球比賽團體決賽實行五場三勝制，且任何一方獲勝三場比賽即結束.甲、乙兩個代表隊最終進入決賽，根據雙方排定的出場順序及以往戰績統計分析，甲隊依次派出的五位選手分別戰勝對手的概率如下表：
出場順序 | 1號 | 2號 | 3號 | 4號 | 5號 |
獲勝概率 |
|
|
|
|
|
若甲隊橫掃對手獲勝（即3∶0獲勝）的概率是
，比賽至少打滿4場的概率為
.
（1）求
，
的值；
（2）求甲隊獲勝場數的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某機構用“10分制”調查了各階層人士對某次國際馬拉松賽事的滿意度，現從調查人群中隨機抽取16名，如圖莖葉圖記錄了他們的滿意度分數
以小數點前的一位數字為莖，小數點后的一位數字為葉
：
（1）指出這組數據的眾數和中位數；
（2）若滿意度不低于
分，則稱該被調查者的滿意度為“極滿意”，求從這16人中隨機選取3人，至少有2人滿意度是“極滿意”的概率；
（3）以這16人的樣本數據來估計整個被調查群體的總體數據，若從該被調查群體人數很多任選3人，記
表示抽到“極滿意”的人數，求的分布列及數學期望．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
