
【題目】已知函數![]() .
.
(Ⅰ)當![]() 時,求
時,求![]() 的單調區間;
的單調區間;
(Ⅱ)若函數![]() 與
與![]() 圖象在
圖象在![]() 上有兩個不同的交點,求實數
上有兩個不同的交點,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)函數![]() 的增區間為
的增區間為 ,減區間
,減區間 ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)將![]() 代入函數
代入函數![]() 的解析式,求出該函數的定義域和導數
的解析式,求出該函數的定義域和導數![]() ,然后分別解不等式
,然后分別解不等式![]() 和
和![]() 可得出函數
可得出函數![]() 的增區間和減區間;
的增區間和減區間;
(Ⅱ)令![]() 得出
得出![]() ,問題轉化為:當直線
,問題轉化為:當直線![]() 與函數
與函數![]() 在區間
在區間![]() 上的圖象有兩個交點時,求實數
上的圖象有兩個交點時,求實數![]() 的取值范圍,并利用導數分析函數
的取值范圍,并利用導數分析函數![]() 在區間
在區間![]() 上的單調性、極值和端點函數值,利用數形結合思想可得出實數
上的單調性、極值和端點函數值,利用數形結合思想可得出實數![]() 的取值范圍,即可求出實數
的取值范圍,即可求出實數![]() 的取值范圍.
的取值范圍.
(Ⅰ)當![]() 時,
時,![]() ,定義域為
,定義域為![]() ,
,
且![]() .
.
令![]() ,即
,即![]() ,解得
,解得![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]() .
.
因此,函數![]() 的增區間為
的增區間為 ,減區間
,減區間 ;
;
(Ⅱ)由已知得:![]() 在
在![]() 有兩個不相等的實數根.
有兩個不相等的實數根.
令![]() ,
,![]() ,由
,由![]() 得
得![]() .
.
當![]() 時,
時,![]() ,此時,函數
,此時,函數![]() 為減函數;
為減函數;
當![]() 時,
時,![]() ,此時,函數
,此時,函數![]() 為增函數.
為增函數.
所以,函數![]() 在
在![]() 處取得極小值
處取得極小值![]() ,
,
又![]() ,
,![]() 且
且![]() ,
,
當![]() 時,直線
時,直線![]() 與函數
與函數![]() 在區間
在區間![]() 上的圖象有兩個交點,
上的圖象有兩個交點,![]() ,
,
因此,實數![]() 的取值范圍是
的取值范圍是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】假設關于某設備的使用年限![]() (年)和所支出的年平均維修費用
(年)和所支出的年平均維修費用![]() (萬元)(即維修費用之和除以使用年限),有如下的統計資料:
(萬元)(即維修費用之和除以使用年限),有如下的統計資料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
維修費用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)畫出散點圖;
(2)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(3)估計使用年限為10年時所支出的年平均維修費用是多少?
參考公式: 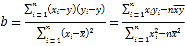
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的離心率為
的離心率為![]() ,頂點為
,頂點為![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)若![]() 是橢圓
是橢圓![]() 上除頂點外的任意一點,直線
上除頂點外的任意一點,直線![]() 交
交![]() 軸于點
軸于點![]() ,直線
,直線![]() 交
交![]() 于點
于點![]() .設
.設![]() 的斜率為
的斜率為![]() ,
,![]() 的斜率為
的斜率為![]() ,試問
,試問![]() 是否為定值?并說明理由.
是否為定值?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設關于某設備的使用年限![]() (年)和所支出的年平均維修費用
(年)和所支出的年平均維修費用![]() (萬元)(即維修費用之和除以使用年限),有如下的統計資料:
(萬元)(即維修費用之和除以使用年限),有如下的統計資料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
維修費用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)畫出散點圖;
(2)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(3)估計使用年限為10年時所支出的年平均維修費用是多少?
參考公式: 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】按照國家質量標準:某種工業產品的質量指標值落在[100,120)內,則為合格品,否則為不合格品.某企業有甲乙兩套設備生產這種產品,為了檢測這兩套設備的生產質量情況,隨機從兩套設備生產的大量產品中各抽取了50件產品作為樣本對規定的質量指標值進行檢測.表1是甲套設備的樣本頻數分布表,圖1是乙套設備的樣本頻率分布直方圖.

質量指標值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
頻數 | 1 | 4 | 19 | 20 | 5 | 1 |
表1:甲套設備的樣本頻數分布表
(1)將頻率視為概率,若乙套設備生產了5000件產品,則其中合格品約有多少件?
(2)填寫下面2×2列聯表,并根據列聯表判斷是否有95%的把握認為這種產品的質量指標值與甲乙兩套設備的選擇有關:
甲套設備 | 乙套設備 | 合計 | |
合格品 | |||
不合格品 | |||
合計 |
(3)根據表和圖,對甲、乙兩套設備的優劣進行比較.參考公式及數據:x2=![]()
P(Х2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱臺![]() 的上下底面分別是邊長為2和4的正方形,
的上下底面分別是邊長為2和4的正方形, ![]() = 4且
= 4且 ![]() ⊥底面
⊥底面![]() ,點
,點![]() 為
為![]() 的中點.
的中點.

(Ⅰ)求證: ![]() 面
面 ![]() ;
;
(Ⅱ)在![]() 邊上找一點
邊上找一點![]() ,使
,使![]() ∥面
∥面![]() ,
,
并求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據市場分析,廣饒縣馳中集團某蔬菜加工點,當月產量在10噸至25噸時,月生產總成本![]() (萬元)可以看成月產量
(萬元)可以看成月產量![]() (噸)的二次函數.當月產量為10噸時,月總成本為20萬元;當月產量為15噸時,月總成本最低為17.5萬元.
(噸)的二次函數.當月產量為10噸時,月總成本為20萬元;當月產量為15噸時,月總成本最低為17.5萬元.
(1)寫出月總成本![]() (萬元)關于月產量
(萬元)關于月產量![]() (噸)的函數關系;
(噸)的函數關系;
(2)已知該產品銷售價為每噸1.6萬元,那么月產量為多少時,可獲最大利潤;
(3)當月產量為多少噸時, 每噸平均成本最低,最低成本是多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知m∈R,命題p:對任意x∈[0,1],不等式x2﹣2x﹣1≥m2﹣3m恒成立,命題q:存在x∈[﹣1,1],使得m≤2x﹣1;
(Ⅰ)若命題p為真命題,求m的取值范圍;
(Ⅱ)若命題q為假命題,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫療器械公司在全國共有![]() 個銷售點,總公司每年會根據每個銷售點的年銷量進行評價分析.規定每個銷售點的年銷售任務為一萬四千臺器械.根據這
個銷售點,總公司每年會根據每個銷售點的年銷量進行評價分析.規定每個銷售點的年銷售任務為一萬四千臺器械.根據這![]() 個銷售點的年銷量繪制出如下的頻率分布直方圖.
個銷售點的年銷量繪制出如下的頻率分布直方圖.
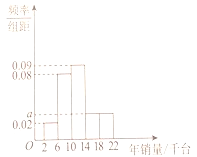
(1)完成年銷售任務的銷售點有多少個?
(2)若用分層抽樣的方法從這![]() 個銷售點中抽取容量為
個銷售點中抽取容量為![]() 的樣本,求該五組
的樣本,求該五組![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(單位:千臺)中每組分別應抽取的銷售點數量.
,(單位:千臺)中每組分別應抽取的銷售點數量.
(3)在(2)的條件下,從該樣本中完成年銷售任務的銷售點中隨機選取![]() 個,求這兩個銷售點不在同一組的概率.
個,求這兩個銷售點不在同一組的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com