
【題目】隨著現(xiàn)代電子技術的迅猛發(fā)展,關于元件和系統(tǒng)可靠性的研究已發(fā)展成為一門新的學科——可靠性理論.在可靠性理論中,一個元件正常工作的概率稱為該元件的可靠性.元件組成系統(tǒng),系統(tǒng)正常工作的概率稱為該系統(tǒng)的可靠性.現(xiàn)有![]() (
(![]() ,
,![]() )種電子元件,每種2個,每個元件的可靠性均為
)種電子元件,每種2個,每個元件的可靠性均為![]() (
(![]() ).當某元件不能正常工作時,該元件在電路中將形成斷路.現(xiàn)要用這
).當某元件不能正常工作時,該元件在電路中將形成斷路.現(xiàn)要用這![]() 個元件組成一個電路系統(tǒng),有如下兩種連接方案可供選擇,當且僅當從A到B的電路為通路狀態(tài)時,系統(tǒng)正常工作.
個元件組成一個電路系統(tǒng),有如下兩種連接方案可供選擇,當且僅當從A到B的電路為通路狀態(tài)時,系統(tǒng)正常工作.
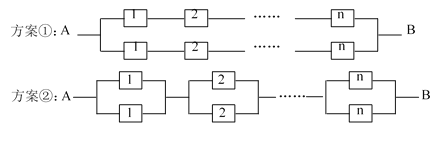
(1)(i)分別寫出按方案①和方案②建立的電路系統(tǒng)的可靠性![]() 、
、![]() (用
(用![]() 和
和![]() 表示);
表示);
(ii)比較![]() 與
與![]() 的大小,說明哪種連接方案更穩(wěn)定可靠;
的大小,說明哪種連接方案更穩(wěn)定可靠;
(2)設![]() ,
,![]() ,已知按方案②建立的電路系統(tǒng)可以正常工作,記此時系統(tǒng)中損壞的元件個數(shù)為
,已知按方案②建立的電路系統(tǒng)可以正常工作,記此時系統(tǒng)中損壞的元件個數(shù)為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
【答案】(1)(i)![]() ,
,![]() (ii)
(ii)![]() ,按方案②建立的電路系統(tǒng)更穩(wěn)定可靠.(2)見解析,
,按方案②建立的電路系統(tǒng)更穩(wěn)定可靠.(2)見解析,![]()
【解析】
(1)(i)利用對立事件的概率公式計算,![]() 個元件串聯(lián)通路的概率是
個元件串聯(lián)通路的概率是![]() ,而
,而![]() 個元件并聯(lián)時不通的概率是
個元件并聯(lián)時不通的概率是![]() ,由此可計算可計算方案①和方案②建立的電路系統(tǒng)的可靠性
,由此可計算可計算方案①和方案②建立的電路系統(tǒng)的可靠性![]() 、
、![]() ;(ii)作差后構造函數(shù)
;(ii)作差后構造函數(shù)![]() ,利用導數(shù)可得其單調性從而得
,利用導數(shù)可得其單調性從而得![]() 與
與![]() 的大小,得出結論;
的大小,得出結論;
(2)在方案②電路系統(tǒng)可以正常工作的條件下,元件損壞的概率是條件概率,可計算編號相同的兩個并聯(lián)元件中至多有一個損壞,且有一個損壞的條件概率為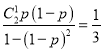 ,由此可知,
,由此可知,![]() ,依次計算出各概率,得分布列,再由二項分布計算出期望.
,依次計算出各概率,得分布列,再由二項分布計算出期望.
解:(1)(i)按方案①建立的電路系統(tǒng)的可靠性![]() ;
;
按方案②建立的電路系統(tǒng)的可靠性為![]() ;
;
(ii)![]() .
.
令![]() ,
,![]() 且
且![]() ,則
,則![]() .
.
當![]() 時,
時,![]() ,從而
,從而![]() ,所以
,所以![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() ,即
,即![]() .
.
所以,![]() ,按方案②建立的電路系統(tǒng)更穩(wěn)定可靠.
,按方案②建立的電路系統(tǒng)更穩(wěn)定可靠.
(2)在方案②電路系統(tǒng)可以正常工作的條件下,編號相同的兩個并聯(lián)元件中至多有一個損壞,且有一個損壞的條件概率為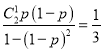 ,由此可知,
,由此可知,![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ;
;
所以,隨機變量![]() 的分布列為
的分布列為
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,其中e為自然對數(shù)的底數(shù).
,其中e為自然對數(shù)的底數(shù).
(1)若函數(shù)![]() 的極小值為
的極小值為![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,證明:當
,證明:當![]() 時,
時,![]() 成立.
成立.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知定點F(1,0),點A在x軸的非正半軸上運動,點B在y軸上運動,滿足![]() 0,A關于點B的對稱點為M,設點M的軌跡為曲線C.
0,A關于點B的對稱點為M,設點M的軌跡為曲線C.
(1)求C的方程;
(2)已知點G(3,﹣2),動直線x=t(t>3)與C相交于P,Q兩點,求過G,P,Q三點的圓在直線y=﹣2上截得的弦長的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD為矩形,平面PCD⊥平面ABCD,AB=2,BC=1,![]() ,E為PB中點.
,E為PB中點.
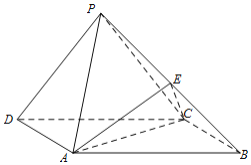
(Ⅰ)求證:PD∥平面ACE;
(Ⅱ)求證:PD⊥平面PBC;
(Ⅲ)求三棱錐E-ABC的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點F是拋物線![]() 的焦點,若點
的焦點,若點![]() 在拋物線C上,且
在拋物線C上,且![]()
(1)求拋物線C的方程;
(2)動直線![]() 與拋物線C相交于
與拋物線C相交于![]() 兩點,問:在x軸上是否存在定點
兩點,問:在x軸上是否存在定點![]() (其中
(其中![]() ),使得x軸平分
),使得x軸平分![]() ?若存在,求出點D的坐標;若不存在,請說明理由.
?若存在,求出點D的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】近年來,國家為了鼓勵高校畢業(yè)生自主創(chuàng)業(yè),出臺了許多優(yōu)惠政策,以創(chuàng)業(yè)帶動就業(yè).某高校畢業(yè)生小李自主創(chuàng)業(yè)從事海鮮的批發(fā)銷售,他每天以每箱300元的價格購入基圍蝦,然后以每箱500元的價格出售,如果當天購入的基圍蝦賣不完,剩余的就作垃圾處理.為了對自己的經(jīng)營狀況有更清晰的把握,他記錄了150天基圍蝦的日銷售量(單位:箱),制成如圖所示的頻數(shù)分布條形圖.

(1)若小李一天購進12箱基圍蝦.
①求當天的利潤![]() (單位:元)關于當天的銷售量
(單位:元)關于當天的銷售量![]() (單位:箱,
(單位:箱,![]() )的函數(shù)解析式;
)的函數(shù)解析式;
②以這150天記錄的日銷售量的頻率作為概率,求當天的利潤不低于1900元的概率;
(2)以上述樣本數(shù)據(jù)作為決策的依據(jù),他計劃今后每天購進基圍蝦的箱數(shù)相同,并在進貨量為11箱,12箱中選擇其一,試幫他確定進貨的方案,以使其所獲的日平均利潤最大.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】橢圓規(guī)是用來畫橢圓的一種器械,它的構造如圖所示,在一個十字形的金屬板上有兩條互相垂直的導槽,在直尺上有兩個固定的滑塊A,B,它們可分別在縱槽和橫槽中滑動,在直尺上的點M處用套管裝上鉛筆,使直尺轉動一周,則點M的軌跡C是一個橢圓,其中|MA|=2,|MB|=1,如圖,以兩條導槽的交點為原點O,橫槽所在直線為x軸,建立直角坐標系.
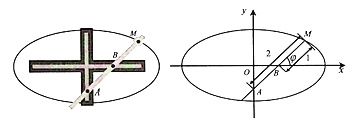
(1)將以射線Bx為始邊,射線BM為終邊的角xBM記為φ(0≤φ<2π),用![]() 表示點M的坐標,并求出C的普通方程;
表示點M的坐標,并求出C的普通方程;
(2)已知過C的左焦點F,且傾斜角為α(0≤α![]() )的直線l1與C交于D,E兩點,過點F且垂直于l1的直線l2與C交于G,H兩點.當
)的直線l1與C交于D,E兩點,過點F且垂直于l1的直線l2與C交于G,H兩點.當![]() ,|GH|,
,|GH|,![]() 依次成等差數(shù)列時,求直線l2的普通方程.
依次成等差數(shù)列時,求直線l2的普通方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,過定點
,過定點![]() 的直線l與橢圓E相交于A,B兩點,C為橢圓的左頂點,當直線l過點
的直線l與橢圓E相交于A,B兩點,C為橢圓的左頂點,當直線l過點![]() 時,
時,![]() (O為坐標原點)的面積為
(O為坐標原點)的面積為![]() .
.
(1)求橢圓E的方程;
(2)求證:當直線l不過C點時,![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在“挑戰(zhàn)不可能”的電視節(jié)目上,甲、乙、丙三個人組成的解密團隊參加一項解密挑戰(zhàn)活動,規(guī)則是由密碼專家給出題目,然后由![]() 個人依次出場解密,每人限定時間是
個人依次出場解密,每人限定時間是![]() 分鐘內(nèi),否則派下一個人.
分鐘內(nèi),否則派下一個人.![]() 個人中只要有一人解密正確,則認為該團隊挑戰(zhàn)成功,否則挑戰(zhàn)失敗.根據(jù)甲以往解密測試情況,抽取了甲
個人中只要有一人解密正確,則認為該團隊挑戰(zhàn)成功,否則挑戰(zhàn)失敗.根據(jù)甲以往解密測試情況,抽取了甲![]() 次的測試記錄,繪制了如下的頻率分布直方圖.
次的測試記錄,繪制了如下的頻率分布直方圖.
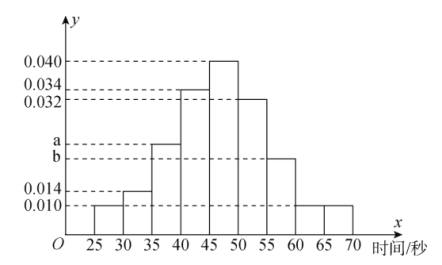
(1)若甲解密成功所需時間的中位數(shù)為![]() ,求
,求![]() 、
、![]() 的值,并求出甲在
的值,并求出甲在![]() 分鐘內(nèi)解密成功的頻率;
分鐘內(nèi)解密成功的頻率;
(2)在“挑戰(zhàn)不可能”節(jié)目上由于來自各方及自身的心理壓力,甲,乙,丙解密成功的概率分別為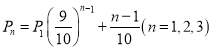 ,其中
,其中![]() 表示第
表示第![]() 個出場選手解密成功的概率,并且
個出場選手解密成功的概率,并且![]() 定義為甲抽樣中解密成功的頻率代替,各人是否解密成功相互獨立.
定義為甲抽樣中解密成功的頻率代替,各人是否解密成功相互獨立.
①求該團隊挑戰(zhàn)成功的概率;
②該團隊以![]() 從小到大的順序按排甲、乙、丙三個人上場解密,求團隊挑戰(zhàn)成功所需派出的人員數(shù)目
從小到大的順序按排甲、乙、丙三個人上場解密,求團隊挑戰(zhàn)成功所需派出的人員數(shù)目![]() 的分布列與數(shù)學期望.
的分布列與數(shù)學期望.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com