【題目】已知二次函數(shù)
的最小值為-1，且關(guān)于
的方程
的兩根為0和-2.
（1）求函數(shù)
的解析式；
（2）設(shè)
其中
，求函數(shù)
在
時的最大值
；
（3）若
（
為實數(shù)），對任意
，總存在
使得
成立，求實數(shù)的取值范圍.
【答案】（1）
；（2）
；（3）
【解析】
（1）根據(jù)方程的根，以及二次函數(shù)的性質(zhì)即可求函數(shù)
的解析式（2）求出
的表達式，結(jié)合二次函數(shù)的圖象和性質(zhì)，即可求函數(shù)在
時的最大值
（3）求出函數(shù)
的值域，利用函數(shù)與方程之間的關(guān)系即可得到結(jié)論．
（1）0，2是方程
的兩根，
，
，
又
最小值即
，
∴
，
，
，
所以.
（2）
，
.
分以下情況討論，的最大值.
（1）當(dāng)
時，
在上是減函數(shù)，
.
（2）當(dāng)
時，的圖像關(guān)于直線
對稱，
∵
，
故只需比較
與
的大小.
當(dāng)
時，即
時，
，
.
當(dāng)
時，即
時，
，
；
綜上所得
.
（3），
函數(shù)的值域為
，
在區(qū)間
上單調(diào)遞增，故值域為
，
對任意
，
總存在
使得
成立，
即
，
解得.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】對任意函數(shù)
，
，可按如圖所示，構(gòu)造一個數(shù)列發(fā)生器，其工作原理如下：
①輸入數(shù)據(jù)
，經(jīng)數(shù)列發(fā)生器輸出
；
②若
，則數(shù)列發(fā)生器結(jié)束工作；若
，將
反饋回輸入端，再輸出
，并依此規(guī)律進行下去.
現(xiàn)定義
.
（1）若輸入
，則由數(shù)列發(fā)生器產(chǎn)生數(shù)列
，寫出數(shù)列的所有項；
（2）若要使數(shù)列發(fā)生器產(chǎn)生一個無窮的常數(shù)列，試求輸入的初始數(shù)據(jù)
的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】湖北省從2021年開始將全面推行新高考制度，新高考“3+1+2”中的“2”要求考生從政治、化學(xué)、生物、地理四門中選兩科，按照等級賦分計入高考成績，等級賦分規(guī)則如下：高考政治、化學(xué)、生物、地理四門等級考試科目的考生原始成績從高到低劃分為A，B，C，D，E五個等級，確定各等級人數(shù)所占比例分別為15%，35%，35%，13%，2%，等級考試科目成績計入考生總成績時，將A至E等級內(nèi)的考生原始成績，依照等比例轉(zhuǎn)換法分別轉(zhuǎn)換到
、
、
、
、
五個分?jǐn)?shù)區(qū)間，得到考生的等級分，等級轉(zhuǎn)換分滿分為100分.具體轉(zhuǎn)換分?jǐn)?shù)區(qū)間如下表：
等級 | A | B | C | D | E |
比例 | 15% | 35% | 35% | 13% | 2% |
賦分區(qū)間 |
|
|
|
|
|
而等比例轉(zhuǎn)換法是通過公式計算：
，其中
、
分別表示原始分區(qū)間的最低分和最高分，
、
分別表示等級分區(qū)間的最低分和最高分，Y表示原始分，T表示轉(zhuǎn)換分，當(dāng)原始分為
、時，等級分分別為、，假設(shè)小明同學(xué)的生物考試成績信息如下表：
考試科目 | 考試成績 | 成績等級 | 原始分區(qū)間 | 等級分區(qū)間 |
生物 | 75分 | B等級 |
|
|
設(shè)小明轉(zhuǎn)換后的等級成績?yōu)?/span>T，根據(jù)公式得：
，所以
（四舍五入取整），小明最終生物等級成績?yōu)?/span>77分.已知某學(xué)校學(xué)生有60人選了政治，以期中考試成績?yōu)樵汲煽冝D(zhuǎn)換該學(xué)校選政治的學(xué)生的政治等級成績，其中政治成績獲得A等級的學(xué)生原始成績統(tǒng)計如下表：
成績 | 90 | 86 | 81 | 80 | 79 | 78 | 75 |
人數(shù) | 1 | 2 | 1 | 1 | 2 | 1 | 1 |
（1）從政治成績獲得A等級的學(xué)生中任取3名，求至少有2名同學(xué)的等級成績不小于93分的概率；
（2）從政治成績獲得A等級的學(xué)生中任取4名，設(shè)4名學(xué)生中等級成績不小于93分人數(shù)為
，求的分布列和期望.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知復(fù)數(shù)z滿足|z|=
的虛部為2，z所對應(yīng)的點在第一象限，
(1)求z;
(2)若z,z2,z-z2在復(fù)平面上對應(yīng)的點分別為A,B,C,求cos∠ABC.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
是定義在
上的奇函數(shù)，且
.
（1）求
的解析式；
（2）判斷的單調(diào)性，并證明你的結(jié)論；
（3）解不等式 
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
．
（Ⅰ）求f（x）的最小正周期和單調(diào)增區(qū)間；
（Ⅱ）當(dāng)x∈[﹣
，
]時，求函數(shù)f（x）的最小值和最大值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，四面體ABCD中，O是BD的中點，CA=CB=CD=BD=2，AB=AD=
．
（1）求證：AO⊥平面BCD；
（2）求異面直線AB與CD所成角的大小；
（3）求二面角O﹣AC﹣D的大小．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某超市花費3萬元購進一批同規(guī)格的月餅，進價為
元/盒.上架銷售前發(fā)現(xiàn)有10盒包裝損壞而不能出售，若能將余下的月餅按高出進價50元/盒全部售出，則可最終獲利8000元.
（1）超市共購進該規(guī)格的月餅多少盒？
（2）現(xiàn)進行促銷活動若顧客一次性購買總價不低于600元的月餅，可在總價的基礎(chǔ)上優(yōu)惠
元但不得低于促銷前總價的9折，求的最大值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)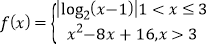
若方程f（x）=m有4個不同的實根x1，x2，x3，x4，且x1＜x2＜x3＜x4，則（
）（x3+x4）=（ ）
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
