
【題目】已知函數![]() .
.
(1)當x∈[1,4]時,求函數![]() 的值域;
的值域;
(2)如果對任意的x∈[1,4],不等式![]() 恒成立,求實數k的取值范圍
恒成立,求實數k的取值范圍
【答案】(1) [0,2]. (2) (-∞,-3).
【解析】
試題分析:(1) 令t=log2x,則函數h(x)轉化為關于t 的二次函數:h(x)=-2(t-1)2+2 ,根據x∈[1,4],得t∈[0,2],結合對稱軸與定義區間位置關系確定函數最值和值域(2) 令t=log2x,則(3-4t)(3-t)>k·t對一切t∈[0,2]恒成立,當t=0時,k∈R;當t∈(0,2]時,利用變量分離法轉化為對應函數最值:![]() 最小值,根據基本不等式求最值:
最小值,根據基本不等式求最值:![]() 即得實數k的取值范圍
即得實數k的取值范圍
試題解析:(1)h(x)=(4-2log2x)·log2x=-2(log2x-1)2+2,
因為x∈[1,4],所以log2x∈[0,2],
故函數h(x)的值域為[0,2].
(2)由f(x2)·f()>k·g(x),
得(3-4log2x)(3-log2x)>k·log2x,
令t=log2x,因為x∈[1,4],所以t=log2x∈[0,2],
所以(3-4t)(3-t)>k·t對一切t∈[0,2]恒成立,
①當t=0時,k∈R;
②當t∈(0,2]時,![]() 恒成立,即
恒成立,即![]() ,因為
,因為![]() ,當且僅當
,當且僅當![]() 即
即![]() 時取等號,所以
時取等號,所以![]() 的最小值為-3,
的最小值為-3,
綜上,k∈(-∞,-3).


 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】已知正方形![]() 的邊長為1,弧
的邊長為1,弧![]() 是以點
是以點![]() 為圓心的圓弧.
為圓心的圓弧.

(1)在正方形內任取一點![]() ,求事件“
,求事件“![]() ”的概率;
”的概率;
(2)用大豆將正方形均勻鋪滿,經清點,發現大豆一共28粒,其中有22粒落在圓中陰影部分內,請據此估計圓周率![]() 的近似值(精確到
的近似值(精確到![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的方程是
的方程是![]() ,圓
,圓![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數).以原點
為參數).以原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(1)分別求直線![]() 與圓
與圓![]() 的極坐標方程;
的極坐標方程;
(2)射線![]() :
:![]() (
(![]() )與圓
)與圓![]() 的交點為
的交點為![]() 、
、![]() 兩點,與直線
兩點,與直線![]() 交于點
交于點![]() ,射線
,射線![]() :
:![]() 與圓
與圓![]() 交于
交于![]() ,
,![]() 兩點,與直線
兩點,與直線![]() 交于點
交于點![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人玩數字游戲,先由甲任想一個數字記為![]() ,再由乙猜甲剛才想的數字把乙想的數字記為
,再由乙猜甲剛才想的數字把乙想的數字記為![]() ,且
,且![]() ,
, ![]() ,記
,記![]() .
.
(1)求![]() 的概率;
的概率;
(2)若![]() ,則稱“甲乙心有靈犀”,求“甲乙心有靈犀”的概率.
,則稱“甲乙心有靈犀”,求“甲乙心有靈犀”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商品進貨價每件50元,據市場調查,當銷售價格(每件x元)在50≤ x ≤80時,每天售出的件數為P=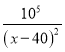 ,每天獲得的利潤為y(元)
,每天獲得的利潤為y(元)
(1)寫出關于x的函數y的表達式;
(2)若想每天獲得的利潤最多,問售價應定為每件多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設關于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是從0,1,2,3四個數中任取的一個數,
是從0,1,2,3四個數中任取的一個數,![]() 是從0,1,2三個數中任取的一個數,求上述方程有實根的概率;
是從0,1,2三個數中任取的一個數,求上述方程有實根的概率;
(2)若![]() 是從區間
是從區間![]() 任取的一個數,
任取的一個數,![]() 是從區間
是從區間![]() 任取的一個數,求上述方程有根的概率.
任取的一個數,求上述方程有根的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com