
【題目】已知函數![]() .
.
(1)若函數![]() 的圖象與x軸相切,求實數a的值;
的圖象與x軸相切,求實數a的值;
(2)討論函數![]() 的零點個數.
的零點個數.
【答案】(1)1(2)當![]() 或
或![]() 時,函數
時,函數![]() 有唯一零點;當
有唯一零點;當![]() 或
或![]() 時,函數
時,函數![]() 有兩個零點.
有兩個零點.
【解析】
(1)令![]() ,求切點
,求切點![]() ,再根據
,再根據![]() 求
求![]() 的值;
的值;
(2)![]()
![]() ,當
,當![]() 時討論函數的單調性,求零點個數,當
時討論函數的單調性,求零點個數,當![]() 時,判斷函數的單調性,可知函數的單調性,并得到函數的最大值
時,判斷函數的單調性,可知函數的單調性,并得到函數的最大值![]() ,設
,設![]() ,根據(1)的單調性,再討論函數的零點個數.
,根據(1)的單調性,再討論函數的零點個數.
(1)![]() ,令
,令![]() ,則
,則![]() ,
,
因為函數![]() 的圖象與x軸相切,所以
的圖象與x軸相切,所以![]() ,
,
即![]() ,
,
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,函數
,函數![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,函數
,函數![]() 單調遞增,所以
單調遞增,所以![]() ,
,
所以![]() 有唯一解
有唯一解![]() ,即實數a的值為1.
,即實數a的值為1.
(2)![]() ,
,
①當![]() 時,
時,![]() ,函數
,函數![]() 在
在![]() 上單調遞增,且
上單調遞增,且![]() ,函數有唯一零點;
,函數有唯一零點;
②當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
![]() ,
,
由(1)![]() 的單調性知:
的單調性知:
(ⅰ)當![]() 時,
時,![]() ,所以函數只有一個零點;
,所以函數只有一個零點;
(ⅱ)當![]() 時,
時,![]() ,
,![]() ,
,
所以函數![]() 在
在![]() 上有一個零點,
上有一個零點,![]() ,
,
令![]() ,則
,則![]() ,
,
所以函數![]() 在
在![]() 上單調遞增,又
上單調遞增,又![]() ,故
,故
當![]() 時,
時,![]() ,所以
,所以![]() ,
,
所以函數![]() 在
在![]() 上有一個零點,
上有一個零點,
所以函數![]() 在
在![]() 上有兩個零點;
上有兩個零點;
(ⅲ)當![]() 時,
時,![]() ,
,![]() ,
,
所以函數![]() 在
在![]() 上有一個零點,
上有一個零點,
當![]() 時,
時,![]() ,
,![]() ,
,
所以函數![]() 在
在![]() 上有一個零點,
上有一個零點,
所以函數![]() 在
在![]() 上有兩個零點,
上有兩個零點,
綜上,當![]() 或
或![]() 時,函數
時,函數![]() 有唯一零點;
有唯一零點;
當![]() 或
或![]() 時,函數
時,函數![]() 有兩個零點.
有兩個零點.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】新疆在種植棉花有著得天獨厚的自然條件,土質呈堿性,夏季溫差大,陽光充足,光合作用充分,生長時間長,這種環境下種植的棉花絨長品質好產量髙,所以新疆棉花舉世聞名.每年五月份,新疆地區進入災害天氣高發期,災害天數對當年棉花產量有著重要影響,根據過去五年的數據統計,得到相關數據如下表:
災害天氣天數 | 2 | 3 | 4 | 5 | 8 |
棉花產量 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根據以上數據,技術人員分別借助甲乙兩種不同的回歸模型,得到兩個回歸方程,
方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)為了評價兩種模型的擬合效果,完成以下任務:① 完成下表;(計算結果精確到0.1)
②分別計算模型甲與模型乙的殘差平方和![]() 及
及![]() ,并比鉸
,并比鉸![]() 的大小,判斷哪個模型擬合效果更好?
的大小,判斷哪個模型擬合效果更好?
災害天氣天數 | 2 | 3 | 4 | 5 | 8 | |
棉花產量 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估計值 | 2.4 | 2.1 | 1.6 | ||
殘差 | 0 |
| 0.1 | |||
模型乙 | 估計值 | 2.3 | 2 | 1.9 | ||
殘差 | 0.1 | 0 | 0 | |||
(2)根據天氣預報,今年五月份新疆![]() 市災害天氣是6天的概率是0.5,災害天氣是7天的概率為0.4,災害天氣是10天的概率為0.1,若何女士在新疆
市災害天氣是6天的概率是0.5,災害天氣是7天的概率為0.4,災害天氣是10天的概率為0.1,若何女士在新疆![]() 市承包了15公頃地種植棉花,請你根據第(1)問中擬合效果較好的模型估計一下何女士今年棉花的產量.(計算過程中所有結果精確到0.01)
市承包了15公頃地種植棉花,請你根據第(1)問中擬合效果較好的模型估計一下何女士今年棉花的產量.(計算過程中所有結果精確到0.01)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明和父母都喜愛《中國好聲音》這欄節目,![]() 年
年![]() 月
月![]() 日晚在鳥巢進行中國好聲音終極決賽,四強選手分別為李榮浩戰隊的邢晗銘,那英戰隊的斯丹曼簇,王力宏戰隊的李芷婷,庾澄慶戰隊的陳其楠,決賽后四位選手相應的名次為
日晚在鳥巢進行中國好聲音終極決賽,四強選手分別為李榮浩戰隊的邢晗銘,那英戰隊的斯丹曼簇,王力宏戰隊的李芷婷,庾澄慶戰隊的陳其楠,決賽后四位選手相應的名次為![]() 、
、![]() 、
、![]() 、
、![]() ,某網站為提升娛樂性,邀請網友在比賽結束前對選手名次進行預測.現用
,某網站為提升娛樂性,邀請網友在比賽結束前對選手名次進行預測.現用![]() 、
、![]() 、
、![]() 、
、![]() 表示某網友對實際名次為
表示某網友對實際名次為![]() 、
、![]() 、
、![]() 、
、![]() 的四位選手名次做出的一種等可能的預測排列,
的四位選手名次做出的一種等可能的預測排列,![]() 是該網友預測的名次與真實名次的偏離程度的一種描述.
是該網友預測的名次與真實名次的偏離程度的一種描述.
(1)求![]() 的分布列及數學期望;
的分布列及數學期望;
(2)按(1)中的結果,若小明家三人的排序號與真實名次的偏離程度都是![]() ,計算出現這種情況的概率(假定小明家每個人排序相互獨立).
,計算出現這種情況的概率(假定小明家每個人排序相互獨立).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左,右焦點分別是
的左,右焦點分別是![]() ,
,![]() ,離心率為
,離心率為![]() ,直線
,直線![]() 被橢圓C截得的線段長為
被橢圓C截得的線段長為![]() .
.
(1)求橢圓C的方程;
(2)過點![]() 且斜率為k的直線l交橢圓C于A,B兩點,交x軸于P點,點A關于x軸的對稱點為M,直線BM交x軸于Q點.求證:
且斜率為k的直線l交橢圓C于A,B兩點,交x軸于P點,點A關于x軸的對稱點為M,直線BM交x軸于Q點.求證:![]() (O為坐標原點)為常數.
(O為坐標原點)為常數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】無窮數列![]() 滿足:
滿足:![]() ,且對任意正整數
,且對任意正整數![]() ,
,![]() 為前
為前![]() 項
項![]() ,
,![]() ,…,
,…,![]() 中等于
中等于![]() 的項的個數.
的項的個數.
(1)直接寫出![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)求證:該數列中存在無窮項的值為1;
(3)已知 ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是正方形,點
是正方形,點![]() 在以
在以![]() 為直徑的半圓弧上(
為直徑的半圓弧上(![]() 不與
不與![]() ,
,![]() 重合),
重合),![]() 為線段
為線段![]() 的中點,現將正方形
的中點,現將正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
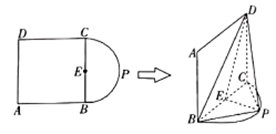
(1)證明:![]() 平面
平面![]() .
.
(2)若![]() ,當三棱錐
,當三棱錐![]() 的體積最大時,求
的體積最大時,求![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 有兩個不同的極值點
有兩個不同的極值點![]() .
.
(1)求![]() 的取值范圍.
的取值范圍.
(2)求![]() 的極大值與極小值之和的取值范圍.
的極大值與極小值之和的取值范圍.
(3)若![]() ,則
,則![]() 是否有最小值?若有,求出最小值;若沒有,說明理由.
是否有最小值?若有,求出最小值;若沒有,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱柱![]() 的底面
的底面![]() 是正方形,側面
是正方形,側面![]() 是矩形,
是矩形,![]() ,
,![]() 為
為![]() 的中點,平面
的中點,平面![]() 平面
平面![]() .
.
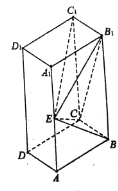
(1)證明:![]() 平面
平面![]() ;
;
(2)判斷二面角![]() 是否為直二面角,不用說明理由;
是否為直二面角,不用說明理由;
(3)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動點![]() 到定點
到定點![]() 的距離之和為4.
的距離之和為4.
(1)求動點![]() 的軌跡方程
的軌跡方程![]()
(2)若軌跡![]() 與直線
與直線![]() 交于
交于![]() 兩點,且
兩點,且![]() 求
求![]() 的值.
的值.
(3)若點![]() 與點
與點![]() 在軌跡
在軌跡![]() 上,且點
上,且點![]() 在第一象限,點
在第一象限,點![]() 在第二象限,點
在第二象限,點![]() 與點
與點![]() 關于原點對稱,求證:當
關于原點對稱,求證:當![]() 時,三角形
時,三角形![]() 的面積為定值.
的面積為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com