
(1)在區間[-2,6]上畫出函數f(x)的圖象.
(2)設集合A={x|f(x)≥5},B=(-∞,-2]∪[0,4]∪[6,+∞).試判斷集合A和B之間的關系,并給出證明.
(3)當k>2時,求證:在區間[-1,5]上,y=kx+3k的圖象位于函數f(x)圖象的上方.
(1)解析:
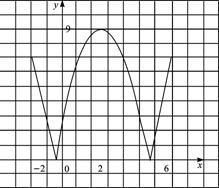
(2)解析:方程f(x)=5的解分別是2-![]() ,0,4和2+
,0,4和2+![]() ,由于f(x)在(-∞,-1]和[2,5]上單調遞減,在[-1,2]和[5,+∞)上單調遞增,因此
,由于f(x)在(-∞,-1]和[2,5]上單調遞減,在[-1,2]和[5,+∞)上單調遞增,因此
A=(-∞,2-![]() ]∪[0,4]∪[2+
]∪[0,4]∪[2+![]() ,+∞).
,+∞).
由于2+![]() <6,2-
<6,2-![]() >-2,∴B
>-2,∴B![]() A.
A.
(3)證明:當x∈[-1,5]時,f(x)=-x2+4x+5.
g(x)=k(x+3)-(-x2+4x+5)
=x2+(k-4)x+(3k-5)
=(x-![]() )2-
)2-![]() ,
,
∵k>2,∴![]() <1.又-1≤x≤5,
<1.又-1≤x≤5,
①當-1≤![]() <1,即2<k≤6時,取x=
<1,即2<k≤6時,取x=![]() .
.
g(x)min=-![]() =-
=-![]() [(k-10)2-64].
[(k-10)2-64].
∵16≤(k-10)2<64,
∴(k-10)2-64<0,
則g(x)min>0.
②當![]() <-1,即k>6時,取x=-1,g(x)min=2k>0.
<-1,即k>6時,取x=-1,g(x)min=2k>0.
由①、②可知,當k>2時,g(x)>0,x∈[-1,5].
因此,在區間[-1,5]上,y=k(x+3)的圖象位于函數f(x)圖象的上方.


 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學業水平測試系列答案
浙江之星學業水平測試系列答案科目:高中數學 來源: 題型:
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| x |
| 2e |
| x |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
| 4 |
| 15 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:徐州模擬 題型:解答題
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com