Question

【題目】某公園為了美化環(huán)境和方便顧客，計劃建造一座圓弧形拱橋，已知該橋的剖面如圖所示，共包括圓弧形橋面和兩條長度相等的直線型路面、，橋面跨度的長不超過米，拱橋所在圓的半徑為米，圓心在水面上，且和所在直線與圓分別在連結(jié)點和處相切.設(shè)，已知直線型橋面每米修建費用是元，弧形橋面每米修建費用是元.

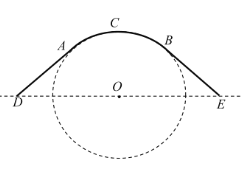
（1）若橋面（線段、和弧）的修建總費用為元，求關(guān)于的函數(shù)關(guān)系式；

（2）當(dāng)為何值時，橋面修建總費用最低？

Answer 1

【答案】（1），.（2）

【解析】

（1）設(shè)為弧的中點，連結(jié)，，，通過解直角三角形以及弧長公式，求得的長，由此計算出修建總費用的表達(dá)式，根據(jù)長度的限制，和圓的直徑，求得的取值范圍.

（2）利用導(dǎo)數(shù)求得的單調(diào)區(qū)間，進(jìn)而求得當(dāng)為何值時，取得最小值.

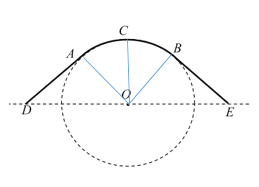
（1）設(shè)為弧的中點，連結(jié)，，，則

在中，.

又因為，所以弧長為，

所以

當(dāng)時，；當(dāng)時，，所以

所以，.

（2）設(shè)，則，令得

當(dāng)時，，函數(shù)單調(diào)遞減；

當(dāng)時，，函數(shù)單調(diào)遞增；

所以當(dāng)時，函數(shù)取得最小值，此時橋面修建總費用最低.