
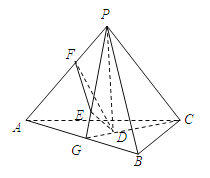
【題目】如圖,已知正三棱錐P-ABC的側面是直角三角形,PA=6,頂點P在平面ABC內的正投影為點D,D在平面PAB內的正投影為點E,連結PE并延長交AB于點G.

(Ⅰ)證明:G是AB的中點;
(Ⅱ)在圖中作出點E在平面PAC內的正投影F(說明作法及理由),并求四面體PDEF的體積.
【答案】(Ⅰ)見解析;(Ⅱ)作圖見解析,體積為![]() .
.
【解析】試題分析:證明![]() 由
由![]() 可得
可得![]() 是
是![]() 的中點.(Ⅱ)在平面
的中點.(Ⅱ)在平面![]() 內,過點
內,過點![]() 作
作![]() 的平行線交
的平行線交![]() 于點
于點![]() ,
, ![]() 即為
即為![]() 在平面
在平面![]() 內的正投影.根據正三棱錐的側面是直角三角形且
內的正投影.根據正三棱錐的側面是直角三角形且![]() ,可得
,可得![]() 在等腰直角三角形
在等腰直角三角形![]() 中,可得
中,可得![]() 四面體
四面體![]() 的體積
的體積![]()
試題解析:(Ⅰ)因為![]() 在平面
在平面![]() 內的正投影為
內的正投影為![]() ,所以
,所以![]()
因為![]() 在平面
在平面![]() 內的正投影為
內的正投影為![]() ,所以
,所以![]()
所以![]() 平面
平面![]() ,故
,故![]()
又由已知可得, ![]() ,從而
,從而![]() 是
是![]() 的中點.
的中點.
(Ⅱ)在平面![]() 內,過點
內,過點![]() 作
作![]() 的平行線交
的平行線交![]() 于點
于點![]() ,
, ![]() 即為
即為![]() 在平面
在平面![]() 內的正投影.
內的正投影.
理由如下:由已知可得![]()
![]() ,
, ![]() ,又
,又![]() ,所以
,所以![]() ,因此
,因此![]() 平面
平面![]() ,即點
,即點![]() 為
為![]() 在平面
在平面![]() 內的正投影.
內的正投影.
連結![]() ,因為
,因為![]() 在平面
在平面![]() 內的正投影為
內的正投影為![]() ,所以
,所以![]() 是正三角形
是正三角形![]() 的中心.
的中心.
由(Ⅰ)知, ![]() 是
是![]() 的中點,所以
的中點,所以![]() 在
在![]() 上,故
上,故![]()
由題設可得![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,因此
,因此![]()
由已知,正三棱錐的側面是直角三角形且![]() ,可得
,可得![]()
在等腰直角三角形![]() 中,可得
中,可得![]()
所以四面體![]() 的體積
的體積![]()


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.
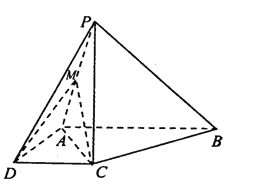
(1)求證: ![]() 平面
平面![]() ;
;
(2)若![]() 為線段
為線段![]() 的中點,且過
的中點,且過![]() 三點的平面與線段
三點的平面與線段![]() 交于點
交于點![]() ,確定點
,確定點![]() 的位置,說明理由;并求三棱錐
的位置,說明理由;并求三棱錐![]() 的高.
的高.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知m>0,p:(x+2)(x-6)≤0,q:2-m≤x≤2+m.
(1)若p是q成立的必要不充分條件,求實數m的取值范圍;
(2)若![]() 是
是![]() 成立的充分不必要條件,求實數m的取值范圍.
成立的充分不必要條件,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() )的離心率為
)的離心率為![]() ,
, ![]() ,
, ![]() 分別是它的左、右焦點,且存在直線
分別是它的左、右焦點,且存在直線![]() ,使
,使![]() ,
, ![]() 關于
關于![]() 的對稱點恰好是圓
的對稱點恰好是圓![]() :
: ![]() (
(![]() ,
, ![]() )的一條直徑的兩個端點.
)的一條直徑的兩個端點.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() 、
、![]() 兩點,射線
兩點,射線![]() 、
、![]() 與橢圓
與橢圓![]() 分別相交于
分別相交于![]() 、
、![]() .試探究:是否存在數集
.試探究:是否存在數集![]() ,當且僅當
,當且僅當![]() 時,總存在
時,總存在![]() ,使點
,使點![]() 在以線段
在以線段![]() 為直徑的圓內?若存在,求出數集
為直徑的圓內?若存在,求出數集![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2016·懷仁期中)已知命題![]() :x∈[-1,2],函數f(x)=x2-x的值大于0.若
:x∈[-1,2],函數f(x)=x2-x的值大于0.若![]() ∨
∨![]() 是真命題,則命題
是真命題,則命題![]() 可以是( )
可以是( )
A. x∈(-1,1),使得cos x<![]()
B. “-3<m<0”是“函數f(x)=x+log2x+m在區間![]() 上有零點”的必要不充分條件
上有零點”的必要不充分條件
C. 直線x=![]() 是曲線f(x)=
是曲線f(x)=![]() 的一條對稱軸
的一條對稱軸
D. 若x∈(0,2),則在曲線f(x)=ex(x-2)上任意一點處的切線的斜率不小于-1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com