
【題目】設橢圓![]() :
:![]() (
(![]() ),左、右焦點分別是
),左、右焦點分別是![]() 、
、![]() 且
且![]() ,以
,以![]() 為圓心,3為半徑的圓與以
為圓心,3為半徑的圓與以![]() 為圓心,1為半徑的圓相交于橢圓
為圓心,1為半徑的圓相交于橢圓![]() 上的點
上的點![]()
(1)求橢圓![]() 的方程;
的方程;
(2)設橢圓![]() :
:![]() ,
,![]() 為橢圓
為橢圓![]() 上任意一點,過點
上任意一點,過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,射線
兩點,射線![]() 交橢圓
交橢圓![]() 于點
于點![]()
①求![]() 的值;
的值;
②令![]() ,求
,求![]() 的面積
的面積![]() 的最大值.
的最大值.
【答案】(1)![]() (2)①
(2)①![]() ②
②![]()
【解析】
(1)運用圓與圓的位置關系,![]() 和
和![]() 的關系,計算即可得到
的關系,計算即可得到![]() ,進而得到橢圓
,進而得到橢圓![]() 的方程;
的方程;
(2)求得橢圓![]() 的方程,①設
的方程,①設![]() ,
,![]() ,求得
,求得![]() 的坐標,分別代入橢圓
的坐標,分別代入橢圓![]() 的方程,化簡整理,即可得到所求值;
的方程,化簡整理,即可得到所求值;
②設![]() ,
,![]() 將直線
將直線![]() 代入橢圓
代入橢圓![]() 的方程,運用韋達定理,三角形的面積公式,將直線
的方程,運用韋達定理,三角形的面積公式,將直線![]() 代入橢圓
代入橢圓![]() 的方程,由判別式大于0,可得
的方程,由判別式大于0,可得![]() 的范圍,結合二次函數的最值,,
的范圍,結合二次函數的最值,,![]() 的面積為
的面積為![]() ,即可得到所求的最大值.
,即可得到所求的最大值.
解:(1)由題意可知,![]() ,可得
,可得![]() ,
,
又![]()
![]() ,
,
![]() ,
,
![]()
即有橢圓![]() 的方程為
的方程為![]() ;
;
(2)由(1)知橢圓![]() 的方程為
的方程為![]() ,
,
①設![]() ,
,![]() ,由題意可知,
,由題意可知,
![]() ,由于
,由于![]() ,
,
代入化簡可得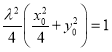 ,
,
所以![]() ,即
,即![]() ;
;
②設![]() ,
,![]() ,將直線
,將直線![]() 代入橢圓
代入橢圓![]() 的方程,可得
的方程,可得
![]()
![]() ,由
,由![]() ,可得
,可得![]() ,③
,③
則有![]() ,
,![]() ,
,
所以![]() ,
,
由直線![]() 與
與![]() 軸交于
軸交于![]() ,
,
則![]() 的面積為
的面積為![]()
![]()
設![]() ,則
,則![]() ,
,
將直線![]() 代入橢圓
代入橢圓![]() 的方程,
的方程,
可得![]()
![]() ,
,
由![]() 可得
可得![]() ,④
,④
由③④可得![]() ,則
,則![]() 在
在![]() 遞增,即有
遞增,即有![]() 取得最大值,
取得最大值,
即有![]() ,即
,即![]() ,取得最大值
,取得最大值![]() ,
,
由①知,![]() 的面積為
的面積為![]() ,
,
即![]() 面積的最大值為
面積的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某校高二理科1班共有50名學生參加學業水平模擬考試,成績(單位:分,滿分100分)大于或等于90分的為優秀,其中語文成績近似服從正態分布![]() ,數學成績的頻率分布直方圖如圖.
,數學成績的頻率分布直方圖如圖.
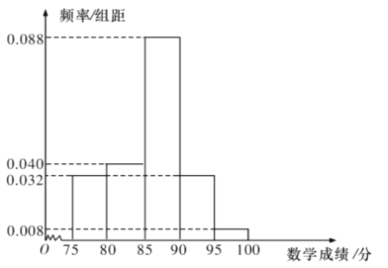
(1)這50名學生中本次考試語文、數學成績優秀的大約各有多少人?
(2)如果語文和數學兩科成績都優秀的共有4人,從語文優秀或數學優秀的這些同學中隨機抽取3人,設3人中兩科都優秀的有X人,求X的分布列和數學期望;
(3)根據(1)(2)的數據,是否有99%以上的把握認為語文成績優秀的同學,數學成績也優秀?
語文優秀 | 語文不優秀 | 合計 | |
數學優秀 | |||
數學不優秀 | |||
合計 |
附:①若![]() ,則
,則![]() ,
,![]() ;②
;②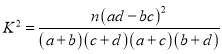 ;
;
③
| 0.1 | 0.05 | 0.025 | 0.010 | p>0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設國家收購某種農產品的價格是1.2元/kg,其中征稅標準為每100元征8元(即稅率為8個百分點,8%),計劃可收購![]() kg.為了減輕農民負擔,決定稅率降低
kg.為了減輕農民負擔,決定稅率降低![]() 個百分點,預計收購可增加
個百分點,預計收購可增加![]() 個百分點.
個百分點.
(1)寫出稅收![]() (元)與
(元)與![]() 的函數關系;
的函數關系;
(2)要使此項稅收在稅率調節后不低于原計劃的78%,確定![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
,![]() )的周期為
)的周期為![]() ,圖象的一個對稱中心為
,圖象的一個對稱中心為![]() 將函數
將函數![]() 圖象上的所有點的橫坐標伸長為原來的2倍(縱坐標不變),再將所有圖象向右平移
圖象上的所有點的橫坐標伸長為原來的2倍(縱坐標不變),再將所有圖象向右平移![]() 個單位長度后得到函數
個單位長度后得到函數![]() 的圖象.
的圖象.
(1)求函數![]() 與
與![]() 的解析式;
的解析式;
(2)當![]() ,求實數
,求實數![]() 與正整數
與正整數![]() ,使
,使![]() 在
在![]() 恰有2019個零點.
恰有2019個零點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方體![]() 的棱長為
的棱長為![]() ,點E,F,G分別為棱AB,
,點E,F,G分別為棱AB,![]() ,
,![]() 的中點,下列結論中,正確結論的序號是___________.
的中點,下列結論中,正確結論的序號是___________.
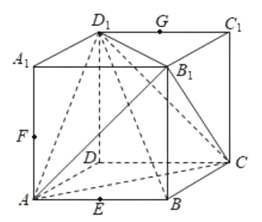
①過E,F,G三點作正方體的截面,所得截面為正六邊形;
②![]() 平面EFG;
平面EFG;
③![]() 平面
平面![]() ;
;
④異面直線EF與![]() 所成角的正切值為
所成角的正切值為![]() ;
;
⑤四面體![]() 的體積等于
的體積等于![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知實數![]() ,
,![]() ,對于定義在
,對于定義在![]() 上的函數
上的函數![]() ,有下述命題:
,有下述命題:
①“![]() 是奇函數”的充要條件是“函數
是奇函數”的充要條件是“函數![]() 的圖像關于點
的圖像關于點![]() 對稱”;
對稱”;
②“![]() 是偶函數”的充要條件是“函數
是偶函數”的充要條件是“函數![]() 的圖像關于直線
的圖像關于直線![]() 對稱”;
對稱”;
③“![]() 是
是![]() 的一個周期”的充要條件是“對任意的
的一個周期”的充要條件是“對任意的![]() ,都有
,都有![]() ”;
”;
④“函數![]() 與
與![]() 的圖像關于
的圖像關于![]() 軸對稱”的充要條件是“
軸對稱”的充要條件是“![]() ”
”
其中正確命題的序號是( )
A.①②B.②③C.①④D.③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在新冠肺炎疫情的影響下,南充高中響應“停課不停教,停課不停學”的號召進行線上教學,高二年級的甲乙兩個班中,需根據某次數學測試成績選出某班的5名學生參加數學競賽決賽,已知這次測試他們取得的成績的莖葉圖如圖所示,其中甲班5名學生成績的平均分是83,乙班5名學生成績的中位數是86.
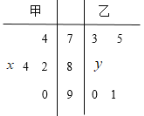
(1)求出x,y的值,且分別求甲乙兩個班中5名學生成績的方差![]() ,并根據結
,并根據結
果,你認為應該選派哪一個班的學生參加決賽?
(2)從成績在85分及以上的學生中隨機抽取2名.求至少有1名來自甲班的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com