Question

【題目】已知函數(shù)f（x）=（x+1）lnx，g（x）=a（x﹣1）（a∈R）．
（Ⅰ）求f（x）的單調區(qū)間；
（Ⅱ）若f（x）≥g（x）對任意的x∈[1，+∞）恒成立，求實數(shù)a的取值范圍；
（Ⅲ）求證：ln2ln3…lnn＞ （n≥2，n∈N+）．

Answer 1

【答案】解：（Ⅰ）f（x）的定義域為（0，+∞），f′（x）=lnx+ +1，

設g（x）=f′（x），g′（x）= ，

令g′（x）＞0，得x＞1，g′（x）＜0，得0＜x＜1，

∴g（x）在（0，1）遞減，在（1，+∞）遞增，g（x）min=g（1）=2，

∴f′（x）＞0在（0，+∞）上恒成立，

∴f（x）的遞增區(qū)間為（0，+∞），無遞減區(qū)間．

（Ⅱ）設h（x）=（x﹣1）lnx﹣ax+a，

由（Ⅰ）知：h′（x）=lnx+ =1﹣a=g（x）﹣a，

g（x）在（1，+∞）遞增，∴g（x）≥g（1）=2，

（i）當a≤2時，h′（x）≥0，h（x）在[1，+∞）遞增，

∴h（x）≥h（1）=0，滿足題意．

（ii）當a＞2時，設ω（x）=h′（x），ω′（x）= ，

當x≥1時，ω′（x）≥0，∴ω（x）在[1，+∞）遞增，

ω（1）=2﹣a＜0，ω（ea）=1+e﹣a＞0，

∴x0∈（1，ea），使ω（x0）=0，∵ω（x）在[1，+∞）遞增，

∴x∈（1，x0），ω（x）＜0，即h′（x）＜0，

∴當x∈（1，x0時，h（x）＜h（1）=0，不滿足題意．

綜上，a的取值范圍為（﹣∞，2]．

（Ⅲ）由（Ⅱ）知，令a=2，（x+1）lnx≥2（x﹣1），

∴x≥1，lnx≥ （當且僅當x=1取“=”），

令x=n（n≥2，n∈N*）得lnn＞ ，

即ln2＞ ，ln3＞ ，ln4＞ ，…，

ln（n﹣2）＞ ，ln（n﹣1）＞ ，lnn＞ ，

將上述n﹣1個式子相乘得：ln2ln3…lnn＞ = ，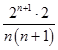

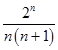∴原命題得證

【解析】（Ⅰ）求出函數(shù)的導數(shù)，解關于導函數(shù)的不等式，求出函數(shù)的單調區(qū)間即可；（Ⅱ）求出h（x）的導數(shù)，通過討論a的范圍，結合函數(shù)的單調性確定a的具體范圍即可；（Ⅲ）得到lnx≥ ，令x=n（n≥2，n∈N*），得lnn＞ ，x取不同的值，相乘即可．
【考點精析】本題主要考查了利用導數(shù)研究函數(shù)的單調性的相關知識點，需要掌握一般的,函數(shù)的單調性與其導數(shù)的正負有如下關系： 在某個區(qū)間內，(1)如果，那么函數(shù)在這個區(qū)間單調遞增；(2)如果，那么函數(shù)在這個區(qū)間單調遞減才能正確解答此題．