
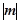
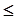 2,�E�A
2,�E�A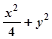 =1��p�ڙE�A���Ƅӣ���
=1��p�ڙE�A���Ƅӣ���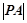 ����Сֵ.
����Сֵ. �C���Ԝyϵ�д�
�C���Ԝyϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
��Ŀ�����Д�(sh��)�W ��Դ����Ԕ �}�ͣ�����}
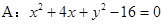 �����c
�����c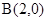 ���cQ�LjAA�ϵĄ��c���cG��BQ�ϣ��cP��QA�ϣ��ҝM��
���cQ�LjAA�ϵĄ��c���cG��BQ�ϣ��cP��QA�ϣ��ҝM��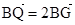 ��
��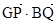 =0��
=0��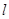 �c����C����M��N���c��ֱ��
�c����C����M��N���c��ֱ��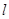 �cy�S����E�c����
�cy�S����E�c����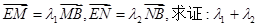 �鶨ֵ��
�鶨ֵ���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ����Ԕ �}�ͣ����x�}
 �����
����� ����Сֵ��m���t�M��
����Сֵ��m���t�M�� �����c
�����c ����(sh��)�� �� ��
����(sh��)�� �� ��| A��5 | B��7 | C��9 | D��11 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ����Ԕ �}�ͣ�����}
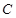 :
: 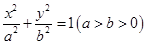 �^�c��0��4�����x���ʞ�
�^�c��0��4�����x���ʞ�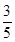 ��
��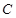 �ķ��̣�
�ķ��̣�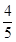 ��ֱ����
��ֱ����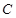 ���ؾ��ε����c���ˣ�
���ؾ��ε����c���ˣ��鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ����Ԕ �}�ͣ�����}
 ,
,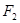 �ǙE�A
�ǙE�A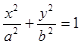
 ���ҽ��c�������x����
���ҽ��c�������x����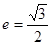 ���ұ�ֱ��
���ұ�ֱ�� ���صõľ��ε����c�ęM���˞�
���صõľ��ε����c�ęM���˞�
 ����E�A�ϵ�����һ�c����
����E�A�ϵ�����һ�c���� ���g�Ǖr����
���g�Ǖr����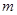 ��ȡֵ������
��ȡֵ�������鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ����Ԕ �}�ͣ�����}
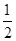 �ęE�AE��һ�����c��AC��x2+y2-4x+2=0�ĈA��.
�ęE�AE��һ�����c��AC��x2+y2-4x+2=0�ĈA��.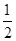 ��ֱ��l1��l2.��ֱ��l1��l2���c�AC���Еr����P������.
��ֱ��l1��l2.��ֱ��l1��l2���c�AC���Еr����P������.�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ����Ԕ �}�ͣ�����}
 ,�ҽ�(j��ng)�^�c
,�ҽ�(j��ng)�^�c ,�^�E�A�����c��ֱ��
,�^�E�A�����c��ֱ�� ���E�A��A��B���c����OA��OB����߅��ƽ����߅��OAPB��
���E�A��A��B���c����OA��OB����߅��ƽ����߅��OAPB��  ��ʹ����߅��OAPB����Σ������ڣ����ֱ��
��ʹ����߅��OAPB����Σ������ڣ����ֱ�� �ķ��̡��������ڣ��f�����ɡ�
�ķ��̡��������ڣ��f�����ɡ��鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W ��Դ����Ԕ �}�ͣ�����}
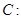
 ���x���ʞ�
���x���ʞ�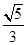 �����c
�����c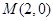 ���E�A���S�Ķ��c��
���E�A���S�Ķ��c��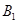 ��
��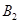 ����
����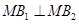 .
.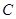 �ķ��̣�
�ķ��̣�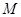 ��б�ʲ���
��б�ʲ���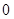 ��ֱ�����E�A
��ֱ�����E�A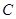 ��
��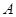 ��
��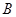 ���c.ԇ��
���c.ԇ��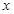 �S���Ƿ���ڶ��c
�S���Ƿ���ڶ��c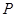 ��ʹ
��ʹ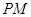 ƽ��
ƽ��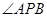 �������ڣ�����c
�������ڣ�����c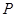 �����ˣ��������ڣ��f������.
�����ˣ��������ڣ��f������.�鿴�𰸺ͽ���>>
���H�WУ��(y��u)�x - �������б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙��e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com