如圖,⊙O是等腰三角形ABC的外接圓,AB=AC,延長BC到點D,使CD=AC,連接AD交⊙O于點E,連接BE與AC交于點F.
⑴判斷BE是否平分∠ABC,并說明理由;
⑵若AE=6,BE=8,求EF的長.
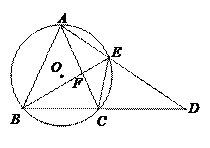
(1)即BE平分∠ABC;(2)EF=

.
⑴BE平分∠ABC.
∵CD=AC,∴∠D="∠CAD."
∵AB=AC,∴∠ABC=∠ACB
∵∠EBC=∠CAD,∴∠EBC="∠D=∠CAD. "
∵∠ABC=∠ABE+∠EBC,∠ACB=∠D+∠CAD,
∴∠ABE=∠EBC,即BE平分∠ABC.
⑵由⑴知∠CAD="∠EBC" =∠ABE.
∵∠AEF=∠AEB,∴△AEF∽△BEA.
∴

,∵
AE=6, BE=8.
∴EF=

.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
如圖
,
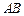
是圓
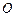
的的直徑,點
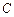
是弧
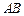
的中點,
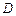
,
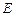
分別是
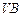
,
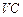
的中點,
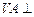
平面
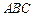
.
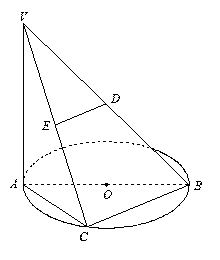
(Ⅰ)求異面直線
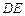
與
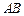
所成的角;
(Ⅱ)證明
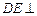
平面
.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
如右圖:
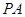
切

于點
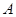
,
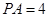
,
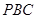
過圓心
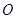
,且與圓相交于
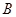
、
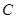
兩點,
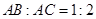
,則

的半徑為
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知
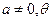
為參數(shù),圓C:
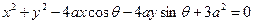
(1)指出圓C的圓心和半徑;(2)求出圓心C的軌跡方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
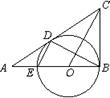
已知:如圖,在△ABC中,∠ABC=90°,O是AB上一點,以O為圓心,OB為半徑的圓與AB交于點E,與AC切于點D,連結DB、DE、OC。若AD=2,AE=1,求CD的長。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
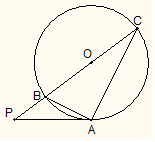
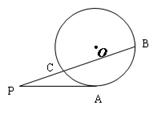
(幾何證明選講選做題) 如圖:PA與圓O相切于A,PCB為圓O的割線,并且不過圓心O,已知∠BPA=
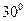
, PA=
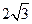
,PC=1,則圓O的半徑等于
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知圓

通過不同的三點
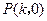
,
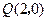
,和
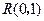
,且該圓在點

處的切線的斜率等于1,求圓

的方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知定點
A(0,1),
B(0,-1),
C(1,0).動點
P滿足:
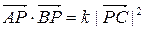
.
(1)求動點
P的軌跡方程,并說明方程表示的曲線類型;
(2)當
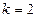
時,求
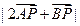
的最大、最小值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
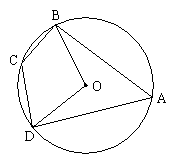
如圖所示,在
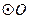
的內(nèi)接四邊形
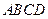
中,
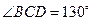
,則
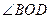
的度數(shù)是____________.
查看答案和解析>>


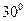 , PA=
, PA=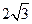 ,PC=1,則圓O的半徑等于 .
,PC=1,則圓O的半徑等于 .
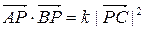 .
.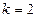 時,求
時,求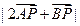 的最大、最小值.
的最大、最小值.