Question

【題目】如圖，正三棱柱ABC﹣A1B1C1的各棱長相等，點D是棱CC1的中點，則AA1與面ABD所成角的大小是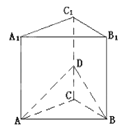

Answer 1

【答案】60°
【解析】解：正三棱柱ABC﹣A1B1C1的各棱長相等，點D是棱CC1的中點，
設棱長為2，以ABC平面內AC順時針旋轉90°得到的直線為x軸，以AC為y軸，以AA1為z軸，
建立如圖所示的空間直角坐標系，
則A（0，0，0），B（2sin30°，2sin60°，0）=（ ， 1，0），D（0，2，1），A1（0，0，2），
∴=（0，0，2），=（0，2，1），=（ ， 1，0），
設平面ABD的法向量為=（x，y，z），
則 ，
∴ ， 解得=（ ， ﹣3，6），
設AA1與面ABD所成角為θ，
則．
∴θ=60°．
故AA1與面ABD所成角的大小是60°．
所以答案是：60°．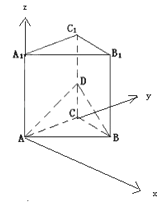

【考點精析】本題主要考查了用空間向量求直線與平面的夾角的相關知識點，需要掌握設直線的方向向量為，平面的法向量為，直線與平面所成的角為，與的夾角為，　則為的余角或的補角的余角.即有：才能正確解答此題．