
【題目】已知f(x)=x3﹣3x+2+m(m>0),在區間[0,2]上存在三個不同的實數a,b,c,使得以f(a),f(b),f(c)為邊長的三角形是直角三角形,則m的取值范圍是 .
【答案】0<m<3+4 ![]()
【解析】解:f(x)=x3﹣3x+3+m,求導f′(x)=3x2﹣3由f′(x)=0得到x=1或者x=﹣1, 又x在[0,2]內,∴函數f(x)在區間(0,1)單調遞減,在區間(1,2)單調遞增,
則f(x)min=f(1)=m+1,f(x)max=f(2)=m+5,f(0)=m+3.
∵在區間[0,2]上存在三個不同的實數a,b,c,使得以f(a),f(b),f(c)為邊長的三角形是構成直角三角形,
∴(m+1)2+(m+1)2<(m+5)2 , 即m2﹣6m﹣23<0,解得3﹣4 ![]() <m<3+4
<m<3+4 ![]()
又已知m>0,∴0<m<3+4 ![]() .
.
所以答案是:0<m<3+4 ![]() .
.
【考點精析】掌握利用導數研究函數的單調性和函數的極值與導數是解答本題的根本,需要知道一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值.
是極小值.


 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案科目:高中數學 來源: 題型:
【題目】正方體![]() 的棱長為1,線段
的棱長為1,線段![]() 上有兩個動點
上有兩個動點![]() , 且
, 且![]() , 則下列結論中錯誤的是( )
, 則下列結論中錯誤的是( )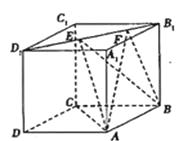
A.![]()
B.三棱錐![]() 的體積為定值
的體積為定值
C.二面角![]() 的大小為定值
的大小為定值
D.異面直線![]() 所成角為定值
所成角為定值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在長方體ABCD﹣A1B1C1D1中AA1=AD=1,E為CD中點.
(Ⅰ)求證:B1E⊥AD1;
(Ⅱ)在棱AA1上是否存在一點P,使得DP∥平面B1AE?若存在,求AP的長;若不存在,說明理由.
(Ⅲ)若二面角A﹣B1E﹣A1的大小為30°,求AB的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是偶函數,且
是偶函數,且![]() ,
,![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的值域;
的值域;
(2)設![]() R,求函數
R,求函數![]() 的最小值
的最小值![]() ;
;
(3)對(2)中的![]() ,若不等式
,若不等式![]() 對于任意的
對于任意的![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知拋物線C:x2=4y,過點M(0,2)任作一直線與C相交于A,B兩點,過點B作y軸的平行線與直線AO相交于點D(O為坐標原點).
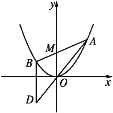
(1)證明動點D在定直線上;
(2)作C的任意一條切線l(不含x軸),與直線y=2相交于點N1,與(1)中的定直線相交于點N2,證明|MN2|2-|MN1|2為定值,并求此定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了增強環保意識,某社團從男生中隨機抽取了60人,從女生中隨機抽取了50人參加環保知識測試,統計數據如下表所示:
優秀 | 非優秀 | 總計 | |
男生 | 40 | 20 | 60 |
女生 | 20 | 30 | 50 |
總計 | 60 | 50 | 110 |
(1)試判斷是否有99%的把握認為環保知識是否優秀與性別有關;
(2)為參加市舉辦的環保知識競賽,學校舉辦預選賽,現在環保測試優秀的同學中選3人參加預選賽,已知在環保測試中優秀的同學通過預選賽的概率為![]() ,若隨機變量
,若隨機變量![]() 表示這3人中通過預選賽的人數,求
表示這3人中通過預選賽的人數,求![]() 的分布列與數學期望.
的分布列與數學期望.
附:![]() =
=![]()
| 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
| 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個命題,其中正確的命題是____.(填出所有正確命題的序號)
①x=![]() 是y=sin(2x+
是y=sin(2x+![]() )的一條對稱軸;
)的一條對稱軸;
②y=esin2x是以π為周期在(0,![]() )上的增函數;
)上的增函數;
③函數y=3sin(2x+![]() )的圖象可由y=3sin2x的圖象向左平移
)的圖象可由y=3sin2x的圖象向左平移![]() 個單位得到.
個單位得到.
④設x1、x2是關于x的方程|logax|=k(a>0,a≠1,k>0)的兩根,則x1x2=1;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com