
(1)證明:an>2;
(2)證明:a1+a2+…+an<2(n+a-2);
(3)若xn=![]() ,求數(shù)列{xn}的通項(xiàng)公式
,求數(shù)列{xn}的通項(xiàng)公式
(文)已知數(shù)列{an}和{bn}滿足:a1=![]() ,且an+bn=1,bn+1=
,且an+bn=1,bn+1=![]() (n∈N*).
(n∈N*).
(1)求數(shù)列{an}與{bn}的通項(xiàng)公式;
(2)設(shè)Sn=a1+a2+a2a3+…+anan+1.若對(duì)任意的n∈N*,不等式kSn>bn恒成立,求正整數(shù)k的最小值.
答案:(理)(1)①當(dāng)n=1時(shí),∵a1=a>2,∴命題an>2成立
②假設(shè)n=k時(shí)命題成立,那么有ak>2成立.
當(dāng)n=k+1時(shí),
∵ak+1-2=![]() >0,∴ak+1>2
>0,∴ak+1>2
即當(dāng)n=k+1時(shí)命題成立.
綜上所述,當(dāng)n∈N*時(shí),an>2成立.
(2)∵an+1=![]() ,∴an=
,∴an=![]() (n≥2)
(n≥2)
又∵an-2=![]()
∴an-2<![]() (n≥2).
(n≥2).
∴(a1-2)+(a2-2)+…+(an-2)
≤(a-2)(1+![]() )
)
=(a-2)![]()
=2(a-2)(1![]() )<2(a-2),
)<2(a-2),
∴a1+a2+…+an<2(n+a-2).
(3)解法一:∵an+1=![]() ,
,
∴![]() ,
,
即![]() ,
,
∵xn=![]() ,∴xn+1=2(xn
,∴xn+1=2(xn![]() )
)
即xn=2(xn-1![]() )(n≥2)
)(n≥2)
∴![]() -xn=2(
-xn=2(![]() -xn-1+
-xn-1+![]() )=2(
)=2(![]() -xn-1)2
-xn-1)2
∵![]() -xn=2(
-xn=2(![]() -xn-1)2=2[2(
-xn-1)2=2[2(![]() -xn-2)2]2
-xn-2)2]2
=21+2![]()
=…=![]()
=![]() ,
,
∴xn=![]()
解法二:∵(![]() )2=
)2=![]() (
(![]() -xn+1)
-xn+1)
設(shè)bn=![]() -xn,則b1=
-xn,則b1=![]() ,bn>0,bn+1=2
,bn>0,bn+1=2![]() ,
,
∴l(xiāng)gbn+1=lg2+2lgbn,
∴l(xiāng)gbn+1+lg2=2(1gbn+lg2),即lg2bn+1=2lg2bn
∴{lg2bn}是等比數(shù)列,公比q=2,
lg2b1=lg(1![]() ),
),
lg2bn=2n-1lg(1![]() )=lg(1
)=lg(1![]() )
)![]()
∴2bn=![]() ,即1-2xn=
,即1-2xn=![]() ,
,
∴xn=![]() .
.
(文)(1)由an+bn=1(n∈N*)知bn=1-an,bn+1=1-an+1,
∴1-an+1=![]()
an-an+1=an·an+1,![]() =1,
=1,
∴數(shù)列![]() 是以
是以![]() =4為首項(xiàng)、以1為公差的等差數(shù)列.
=4為首項(xiàng)、以1為公差的等差數(shù)列.
∴![]() =4+n-1=n+3,∴an=
=4+n-1=n+3,∴an=![]() (n∈N*).
(n∈N*).
bn=1-an=1![]() (n∈N*).
(n∈N*).
(2)Sn=a1a2+a2a3+…+anan+1
=![]()
=![]() .
.
對(duì)任意n∈N*,不等式kSn>bn恒成立
∴![]() 即
即![]() 恒成立
恒成立
令f(n)=![]() ,
,
則f(1)=![]() ,f(2)=
,f(2)=![]() ,
,
又當(dāng)n≥3時(shí),n2>8,從而n2+3n>3n+8.
即![]() <1,∴f(n)<2.
<1,∴f(n)<2.
可見對(duì)任意n∈N*,f(n)的最大值為![]() ,故
,故![]() ,
,
∴k的最小值為16.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
| a | 2 n |
| sn |
| (n+50)sn+1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(08年正定中學(xué)一模理) (12分)
設(shè)數(shù)列{an}的各項(xiàng)都是正數(shù),且對(duì)任意n∈N+,都有![]() ,記Sn為數(shù)列{an}的前n項(xiàng)和.
,記Sn為數(shù)列{an}的前n項(xiàng)和.
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)若![]() (
(![]() 為非零常數(shù),n∈N+),問是否存在整數(shù)
為非零常數(shù),n∈N+),問是否存在整數(shù)![]() ,使得對(duì)任意 n∈N+,都有bn+1>bn.
,使得對(duì)任意 n∈N+,都有bn+1>bn.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
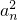 成等差數(shù)列.(1)求通項(xiàng)an;(2)設(shè)
成等差數(shù)列.(1)求通項(xiàng)an;(2)設(shè) 求f(n)的最大值.
求f(n)的最大值.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:甘谷縣模擬 題型:解答題
| a | 2n |
| sn |
| (n+50)sn+1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年甘肅省天水一中、甘谷一中高三(下)第八次聯(lián)考數(shù)學(xué)試卷(解析版) 題型:解答題
 成等差數(shù)列.(1)求通項(xiàng)an;(2)設(shè)
成等差數(shù)列.(1)求通項(xiàng)an;(2)設(shè)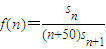 求f(n)的最大值.
求f(n)的最大值.查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com