
��֪���タ(xi��n)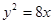 �c�E�A
�c�E�A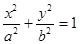 ������c(di��n)
�й������c(di��n)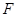 ���ҙE�A�^(gu��)�c(di��n)
���ҙE�A�^(gu��)�c(di��n)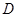
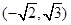 .
.
��1����E�A���̣�
��2���c(di��n) ��
��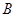 �ǙE�A��������c(di��n)���c(di��n)
�ǙE�A��������c(di��n)���c(di��n)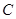 ������c(di��n)��ӛ�^(gu��)�c(di��n)
������c(di��n)��ӛ�^(gu��)�c(di��n) ��
��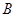 ��
��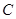 �ĈA���
�ĈA���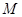 ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)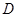 ����
����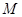 ���о�(xi��n)
���о�(xi��n)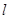 ����ֱ��(xi��n)
����ֱ��(xi��n)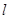 �ķ��̣�
�ķ��̣�
��3���^(gu��)�E�A������c(di��n)�����ഹֱ�ăɗlֱ��(xi��n)�քe���E�A������һ�c(di��n)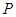 ��
��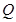 ��ԇ��(w��n)ֱ��(xi��n)
��ԇ��(w��n)ֱ��(xi��n)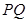 �Ƿ�(j��ng)�^(gu��)���c(di��n)�����ǣ�������c(di��n)����(bi��o)�������ǣ��f(shu��)������.
�Ƿ�(j��ng)�^(gu��)���c(di��n)�����ǣ�������c(di��n)����(bi��o)�������ǣ��f(shu��)������.
��1��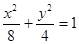 ����2��
����2��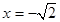 ��
��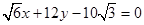 ����3��
����3��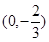 ��
��
����ԇ�}��������1�����}Ŀ�o���ėl��ֱ�����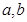 ��ֵ���t������E�A���̣���2����(d��ng)����ֱ��(xi��n)б�ʲ����ڕr(sh��)���䷽�̞�
��ֵ���t������E�A���̣���2����(d��ng)����ֱ��(xi��n)б�ʲ����ڕr(sh��)���䷽�̞�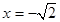 �������}�⣻��(d��ng)ֱ��(xi��n)б�ʴ��ڕr(sh��)�����O(sh��)��б�ʞ�
�������}�⣻��(d��ng)ֱ��(xi��n)б�ʴ��ڕr(sh��)�����O(sh��)��б�ʞ�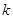 ����(xi��)��ֱ��(xi��n)���c(di��n)бʽ���̣���?y��n)�ֱ��(xi��n)�c�A���У����Ը���(j��)�A�ĵ�ֱ��(xi��n)�ľ��x���ڈA�İ돽��ֱ�����ֱ��(xi��n)��б�ʣ��Ķ��õ����̣���3�����}���֪����ֱ��(xi��n)��б�ʶ����ڣ��O(sh��)AP��
����(xi��)��ֱ��(xi��n)���c(di��n)бʽ���̣���?y��n)�ֱ��(xi��n)�c�A���У����Ը���(j��)�A�ĵ�ֱ��(xi��n)�ľ��x���ڈA�İ돽��ֱ�����ֱ��(xi��n)��б�ʣ��Ķ��õ����̣���3�����}���֪����ֱ��(xi��n)��б�ʶ����ڣ��O(sh��)AP��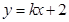 ������E�A�ķ��̏Ķ�����c(di��n)
������E�A�ķ��̏Ķ�����c(di��n)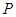 ������(bi��o)��ͬ��������c(di��n)
������(bi��o)��ͬ��������c(di��n)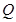 ������(bi��o)���Ķ������ֱ��(xi��n)
������(bi��o)���Ķ������ֱ��(xi��n)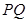 �ķ��̣��ɷ��̿�֪��(d��ng)
�ķ��̣��ɷ��̿�֪��(d��ng)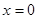 �r(sh��)��
�r(sh��)��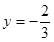 �����������ֱ��(xi��n)���^(gu��)���c(di��n)
�����������ֱ��(xi��n)���^(gu��)���c(di��n)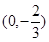 ��
��
ԇ�}������
(1)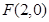 ���tc=2, ��
���tc=2, ��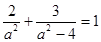 ����
����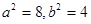
������E�A���̞�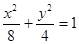 ��
��
(2)M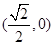 ,��M:
,��M: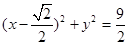 ��ֱ��(xi��n)lб�ʲ����ڕr(sh��)��
��ֱ��(xi��n)lб�ʲ����ڕr(sh��)��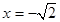 ��
��
ֱ��(xi��n)lб�ʴ��ڕr(sh��)���O(sh��)��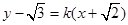 ��
��
��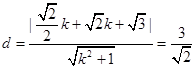 �����
�����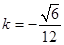 ��
��
��ֱ��(xi��n)l��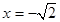 ��
��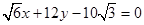 ��
��
��3���@Ȼ����ֱ��(xi��n)б�ʴ���, �O(sh��)AP��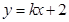 ��
��
����E�A���̣���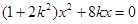 ������c(di��n)
������c(di��n) ��
��
ͬ����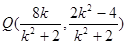 ��ֱ��(xi��n)PQ��
��ֱ��(xi��n)PQ��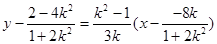 ��
��
��x=0����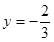 ����ֱ��(xi��n)PQ�^(gu��)���c(di��n)
����ֱ��(xi��n)PQ�^(gu��)���c(di��n)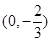 ��
��
���c(di��n)�����}�����˙E�A�Ę�(bi��o)��(zh��n)���̣������˙E�A�ĺ�(ji��n)�Ύ����|(zh��)��������ֱ��(xi��n)�͈A�F����(xi��n)���P(gu��n)ϵ��ͻ�������˔�(sh��)�νY(ji��)�ϡ����(l��i)ӑՓ������(sh��)�c���̡��ȃr(ji��)�D(zhu��n)���Ȕ�(sh��)�W(xu��)˼�뷽����


 ��У�n��ϵ�д�
��У�n��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��13�֣���D��ij�����O(sh��)Ӌ(j��)���p����܇(ch��)����܇(ch��)������20m��Ҫ��ͨ��܇(ch��)�v��5m������ȫ�L(zh��ng)2.5km�������ăɂ�(c��)���c���洹ֱ�ĉ����߶Ȟ�3�ף������ϲ�����(xi��n)���Ƶؿ��ɰ낀(g��)�E�A��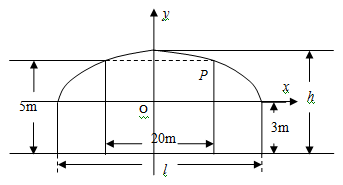
��1�������h(yu��n)��6 m���t�����O(sh��)Ӌ(j��)�Ĺ���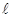 �Ƕ��٣�
�Ƕ��٣�
��2����Ҫʹ�����Ϸ���E�A���ֵ��������� ����С���t��(y��ng)����O(sh��)Ӌ(j��)����h(yu��n)����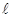 ������֪���E�A
������֪���E�A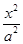 +
+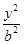 =1����e��ʽ��S=
=1����e��ʽ��S=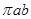 �����w�w�e�����e���Ըߡ���
�����w�w�e�����e���Ըߡ���
��3������ʹ������(n��i)�����^��Ҫ���ڹ���(xi��n)���҃ɂ�(g��)�c(di��n)M��N��ʹ��������λ�õĸ߶�ǡ������5m���F(xi��n)��M��N�Լ��E�A��������c(di��n)��֧�c(di��n)���úϽ�䓰����������(xi��n)�����B�ӷ��]���γ�һ��(g��)���Σ���l=30m�����������ڂ�(c��)���λ��e��䓰���r(ji��)������픲���λ��e䓰���r(ji��)��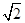 ����ԇ�_��M��N��λ���Լ�
����ԇ�_��M��N��λ���Լ�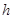 ��ֵ��ʹ����r(ji��)���١�
��ֵ��ʹ����r(ji��)���١�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A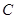 ��������ԭ�c(di��n)
��������ԭ�c(di��n)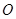 ,�x����
,�x����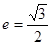 ,�ҽ��c(di��n)��
,�ҽ��c(di��n)��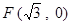 .
.
(��)��E�A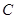 �ķ���;
�ķ���;
(��)�O(sh��)�E�A������c(di��n)��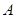 ,�ڙE�A
,�ڙE�A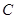 ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)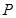 ,ʹ������
,ʹ������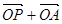 �c
�c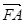 ����(xi��n)?������,��ֱ��(xi��n)
����(xi��n)?������,��ֱ��(xi��n)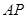 �ķ���;��������,��(ji��n)Ҫ�f(shu��)������.
�ķ���;��������,��(ji��n)Ҫ�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A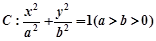 �Ľ��c(di��n)��
�Ľ��c(di��n)��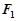
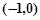 ��
��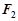
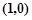 ���ҽ�(j��ng)�^(gu��)�c(di��n)
���ҽ�(j��ng)�^(gu��)�c(di��n)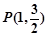 .
.
������E�A �ķ��̣�
�ķ��̣�
�����O(sh��)�^(gu��)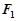 ��ֱ��(xi��n)
��ֱ��(xi��n) �c�E�A
�c�E�A ����
����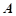 ��
�� ���c(di��n)����(w��n)�ڙE�A
���c(di��n)����(w��n)�ڙE�A ���Ƿ����һ�c(di��n)
���Ƿ����һ�c(di��n) ��ʹ��߅��
��ʹ��߅��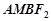 ��ƽ����߅�Σ������ڣ����ֱ��(xi��n)
��ƽ����߅�Σ������ڣ����ֱ��(xi��n) �ķ��̣��������ڣ�Ո(q��ng)�f(shu��)������.
�ķ��̣��������ڣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A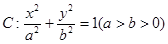 �^(gu��)�c(di��n)
�^(gu��)�c(di��n)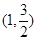 �����x����
�����x����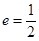 ��
��
������E�A �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
������ֱ��(xi��n)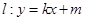 �c�E�A
�c�E�A �ཻ��
�ཻ��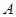 ��
��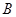 ���c(di��n)��
���c(di��n)��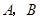 ����������c(di��n)�����E�A������c(di��n)��D���ҝM(m��n)��
����������c(di��n)�����E�A������c(di��n)��D���ҝM(m��n)��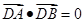 ��ԇ�Д�ֱ��(xi��n)
��ԇ�Д�ֱ��(xi��n)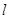 �Ƿ��^(gu��)���c(di��n)�����^(gu��)���c(di��n)�����ԓ���c(di��n)������(bi��o)�������^(gu��)���c(di��n)��Ո(q��ng)�f(shu��)�����ɡ�
�Ƿ��^(gu��)���c(di��n)�����^(gu��)���c(di��n)�����ԓ���c(di��n)������(bi��o)�������^(gu��)���c(di��n)��Ո(q��ng)�f(shu��)�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪���タ(xi��n)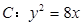 ��
��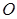 ������(bi��o)ԭ�c(di��n)����(d��ng)ֱ��(xi��n)
������(bi��o)ԭ�c(di��n)����(d��ng)ֱ��(xi��n)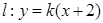 �c
�c
���タ(xi��n)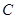 ���ڲ�ͬ���c(di��n)
���ڲ�ͬ���c(di��n)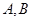
��1�����C: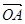 ��
��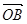 �鳣��(sh��)��
�鳣��(sh��)��
��2����M(m��n)��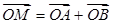 ���c(di��n)
���c(di��n)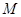 ��܉�E���̡�
��܉�E���̡�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪���タ(xi��n)y2=��x�cֱ��(xi��n)y=k(x+1)����A��B���c(di��n).
��1�����C��OA��OB��
��2����(d��ng)DAOB����e����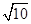 �r(sh��)����k��ֵ.
�r(sh��)����k��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
����(xi��n)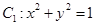 �ھ��
�ھ��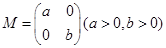 ��׃�Q�����µõ�����(xi��n)
��׃�Q�����µõ�����(xi��n) ��
��
��������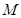 ��
��
��������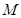 ������ֵ����(du��)��(y��ng)��һ��(g��)����������
������ֵ����(du��)��(y��ng)��һ��(g��)����������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�AC�����Ğ�ֱ������(bi��o)ϵxOy��ԭ�c(di��n)�����c(di��n)��s�S�ϣ�����һ��(g��)��c(di��n)���ɂ�(g��)���c(di��n)�ľ��x�քe��7��1.
������E�AC�ķ��̣�
������P��E�AC�ϵĄ�(d��ng)�c(di��n)��M���^(gu��)P�Ҵ�ֱ��x�S��ֱ��(xi��n)�ϵ��c(di��n)��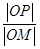 =�ˣ����c(di��n)M��܉�E���̣����f(shu��)��܉�E��ʲô����(xi��n)��
=�ˣ����c(di��n)M��܉�E���̣����f(shu��)��܉�E��ʲô����(xi��n)��
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com