【題目】共享單車因綠色、環保、健康的出行方式，在國內得到迅速推廣.最近，某機構在某地區隨機采訪了10名男士和10名女士，結果男士、女士中分別有7人、6人表示“經常騎共享單車出行”，其他人表示“較少或不選擇騎共享單車出行”.
（1）從這些男士和女士中各抽取一人，求至少有一人“經常騎共享單車出行”的概率；
（2）從這些男士中抽取一人，女士中抽取兩人，記這三人中“經常騎共享單車出行”的人數為
，求
的分布列與數學期望.
科目：高中數學 來源： 題型：
【題目】某校為了鼓勵學生熱心公益，服務社會，成立了“慈善義工社”.2017年12月，該校“慈善義工社”為學生提供了4次參加公益活動的機會，學生可通過網路平臺報名參加活動.為了解學生實際參加這4次活動的情況，該校隨機抽取100名學生進行調查，數據統計如下表，其中“√”表示參加，“×”表示未參加.
（Ⅰ）從該校所有學生中任取一人，試估計其2017年12月恰參加了2次學校組織的公益活動的概率；
（Ⅱ）若在已抽取的100名學生中，2017年12月恰參加了1次活動的學生比4次活動均未參加的學生多17人，求
的值；
（Ⅲ）若學生參加每次公益活動可獲得10個公益積分，試估計該校4000名學生中，2017年12月獲得的公益積分不少于30分的人數.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于集合
，定義了一種運算“
”，使得集合
中的元素間滿足條件：如果存在元素
，使得對任意
，都有
，則稱元素
是集合
對運算“
”的單位元素．例如： 
，運算“
”為普通乘法；存在
，使得對任意
，都有
，所以元素
是集合
對普通乘法的單位元素．
下面給出三個集合及相應的運算“
”：
①
，運算“
”為普通減法；
②
{
表示
階矩陣， 
}，運算“
”為矩陣加法；
③
（其中
是任意非空集合），運算“
”為求兩個集合的交集．
其中對運算“
”有單位元素的集合序號為（ ）
A. ①②； B. ①③； C. ①②③； D. ②③．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖， 
為圓柱
的母線， 
是底面圓
的直徑， 
是
的中點.
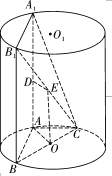
（Ⅰ）問： 
上是否存在點
使得
平面
？請說明理由；
（Ⅱ）在（Ⅰ）的條件下，若
平面
，假設這個圓柱是一個大容器，有條體積可以忽略不計的小魚能在容器的任意地方游弋，如果小魚游到四棱錐
外會有被捕的危險，求小魚被捕的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
， 
（
）.
（1）當
時，若函數
與
的圖象在
處有相同的切線，求
的值；
（2）當
時，若對任意
和任意
，總存在不相等的正實數
，使得
，求
的最小值；
（3）當
時，設函數
與
的圖象交于
兩點．求證： 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將圓
上每個點的橫坐標變為原來的4倍，縱坐標變為原來的3倍，得曲線
，以坐標原點為極點， 
軸的非負軸分別交于
半軸為極軸建立極坐標系，直線
的極坐標方程為： 
，且直線
在直角坐標系中與
軸分別交于
兩點.
（1）寫出曲線
的參數方程，直線
的普通方程；
（2）問在曲線
上是否存在點
，使得
的面積
，若存在，求出點
的坐標，若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在四棱錐PABCD中，AD∥BC，平面PAC⊥平面ABCD，AB=AD=DC=1，
∠ABC=∠DCB=60，E是PC上一點.
（Ⅰ）證明：平面EAB⊥平面PAC；
（Ⅱ）若△PAC是正三角形，且E是PC中點，求三棱錐AEBC的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】橢圓
經過
為坐標原點，線段
的中點在圓
上.
（1）求
的方程；
（2）直線
不過曲線
的右焦點
，與
交于
兩點，且
與圓
相切，切點在第一象限， 
的周長是否為定值？并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
