
【題目】如圖,在棱長為1的正方體![]() 中,
中, ![]() 為線段
為線段![]() 的中點,
的中點,![]() 為線段
為線段![]() 上一動點.
上一動點.
(Ⅰ)求證:![]() ;
;
(Ⅱ)當![]() 時,求三棱錐
時,求三棱錐![]() 的體積;
的體積;
(Ⅲ)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ?說明理由.
?說明理由.
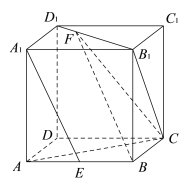
【答案】(1)證明見解析.
(2)![]() .
.
(3)存在;理由見解析.
【解析】
(1)連結![]() ,借助于正方體的特征,結合線面垂直的判定和線面垂直的性質,得到
,借助于正方體的特征,結合線面垂直的判定和線面垂直的性質,得到![]() ;
;
(2)根據題中的條件,確定出對應的點的位置,將三棱錐的頂點和底面轉換,利用體積相等,求得結果;
(3)借助于平行四邊形找到平行線,利用線面平行的判定定理,證得結果.
(Ⅰ)連結![]() .
.
在正方體![]() 中,
中,
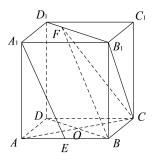
![]() ,
,![]() ,
,
所以![]() .
.
因為![]() 為正方形,
為正方形,![]() ,
,
所以![]() .
.
又因為![]() ,
,
所以![]() .
.
因為,
所以![]() .
.
(Ⅱ)過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() .
.
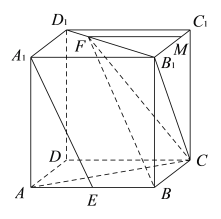
在正方體![]() 中,
中,
因為![]() ,
,
又因為![]() ,
,
所以![]() .
.
所以![]() 為三棱錐
為三棱錐![]() 的高.
的高.
因為![]() ,
,
所以![]() .
.
所以![]()
(III)存在. 當![]() 為
為![]() 中點時,
中點時,![]() 平面
平面![]() .
.
設![]() 為
為![]() 中點,連結
中點,連結![]() .
.
因為![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點,
的中點,
所以![]() .
.
因為![]() ,
,
所以![]() .
.
所以![]() .
.
在正方形![]() 中,
中,
因為![]() 為
為![]() 中點,
中點,
所以![]() ,且
,且![]() .
.
所以四邊形![]() 為平行四邊形.
為平行四邊形.
所以![]()
因為![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】定義非零向量![]() 的“相伴函數”為
的“相伴函數”為![]() (
(![]() ),向量
),向量![]() 稱為函數
稱為函數![]() 的“相伴向量”(其中
的“相伴向量”(其中![]() 為坐標原點),記平面內所有向量的“相伴函數”構成的集合為
為坐標原點),記平面內所有向量的“相伴函數”構成的集合為![]() .
.
(1)已知![]() (
(![]() ),求證:
),求證:![]() ,并求函數
,并求函數![]() 的“相伴向量”模的取值范圍;
的“相伴向量”模的取值范圍;
(2)已知點![]() (
(![]() )滿足
)滿足![]() ,向量
,向量![]() 的 “相伴函數”
的 “相伴函數”![]() 在
在![]() 處取得最大值,當點
處取得最大值,當點![]() 運動時,求
運動時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北京市某年11月1日—20日監測最高最低溫度及差值數據如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
最高溫度(℃) | 20 | 16 | 14 | 20 | 20 | 20 | 18 | 15 | 12 | 11 | 12 | 12 | 13 | 9 | 8 | 6 | 13 | 11 | 10 | 14 |
最低溫度(℃) | 5 | 4 | 2 | 4 | 9 | 6 | 9 | 3 | -1 | 0 | 5 | 1 | 4 | -1 | -4 | -2 | -1 | 0 | 1 | 3 |
差值(℃) | 15 | 12 | 12 | 16 | 11 | 14 | 9 | 12 | 13 | 11 | 7 | 11 | 9 | 10 | 12 | 8 | 14 | 11 | 9 | 11 |
(Ⅰ)完成下面的頻率分布表及頻率分布直方圖,并寫出頻率分布直方圖中![]() 的值;
的值;

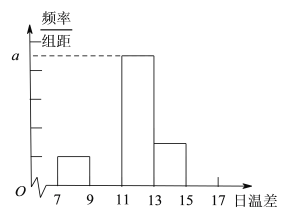
(Ⅱ)從日溫差大于等于![]() 的這些天中,隨機選取2天.求這兩天中至少有一天的溫差在區間
的這些天中,隨機選取2天.求這兩天中至少有一天的溫差在區間![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知x∈(0, ![]() ),則函數f(x)=sinxtanx+cosxcotx的值域為( )
),則函數f(x)=sinxtanx+cosxcotx的值域為( )
A.[1,2)
B.[ ![]() ,+∞)
,+∞)
C.(1, ![]() ]
]
D.[1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班級有50名學生,其中有30名男生和20名女生,隨機詢問了該班五名男生和五名女生在某次數學測驗中的成績,五名男生的成績分別為86,94,88,92,90,五名女生的成績分別為88,93,93,88,93,下列說法正確的是( )
A.這種抽樣方法是一種分層抽樣
B.這種抽樣方法是一種系統抽樣
C.這五名男生成績的方差大于這五名女生成績的方差
D.該班男生成績的平均數大于該班女生成績的平均數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com