
【題目】已知x∈(0, ![]() ),則函數f(x)=sinxtanx+cosxcotx的值域為( )
),則函數f(x)=sinxtanx+cosxcotx的值域為( )
A.[1,2)
B.[ ![]() ,+∞)
,+∞)
C.(1, ![]() ]
]
D.[1,+∞)
 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.
AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.

(I)在平面PAB內找一點M,使得直線CM∥平面PBE,并說明理由;
(II)若二面角P-CD-A的大小為45°,求直線PA與平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,直線
,直線![]() 與平面
與平面![]() 成
成![]() 角,
角, ![]() 為
為![]() 的中點,
的中點, ![]() ,
, ![]() .
.

(Ⅰ)若![]() ,求證:平面
,求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值的取值范圍.
所成角的正弦值的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
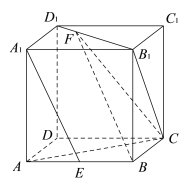
【題目】如圖,在棱長為1的正方體![]() 中,
中, ![]() 為線段
為線段![]() 的中點,
的中點,![]() 為線段
為線段![]() 上一動點.
上一動點.
(Ⅰ)求證:![]() ;
;
(Ⅱ)當![]() 時,求三棱錐
時,求三棱錐![]() 的體積;
的體積;
(Ⅲ)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ?說明理由.
?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】x的取值范圍為[0,10],給出如圖所示程序框圖,輸入一個數x.
(1)請寫出程序框圖所表示的函數表達式;
(2)求輸出的y(y<5)的概率;
(3)求輸出的y(6<y≤8)的概率.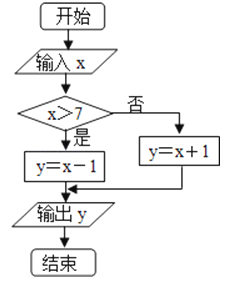
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,
, ![]() .
.
(1)若函數![]() 在
在![]() 上單調遞增,求
上單調遞增,求![]() 的取值范圍;
的取值范圍;
(2)設![]() ,點
,點![]() 是曲線
是曲線![]() 與
與![]() 的一個交點,且這兩曲線在點
的一個交點,且這兩曲線在點![]() 處的切線互相垂直,證明:存在唯一的實數
處的切線互相垂直,證明:存在唯一的實數![]() 滿足題意,且
滿足題意,且![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次趣味校園運動會的頒獎儀式上,高一、高二、高三代表隊人數分別為120人、120人、n人.為了活躍氣氛,大會組委會在頒獎過程中穿插抽獎活動,并用分層抽樣的方法從三個代表隊中共抽取20人在前排就座,其中高二代表隊有6人.

(1)求n的值;
(2)把在前排就座的高二代表隊6人分別記為a,b,c,d,e,f,現隨機從中抽取2人上臺抽獎.求a和b至少有一人上臺抽獎的概率;
(3)抽獎活動的規則是:代表通過操作按鍵使電腦自動產生兩個[0,1]之間的均勻隨機數x,y,并按如圖所示的程序框圖執行.若電腦顯示“中獎”,則該代表中獎;若電腦顯示“謝謝”,則不中獎,求該代表中獎的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com