
(Ⅰ)證明c2=ab,并求直線BF與y軸的交點M的坐標;
(Ⅱ)設直線BF交橢圓于P、Q兩點,證明![]() ·
·![]() =
=![]() b2.
b2.
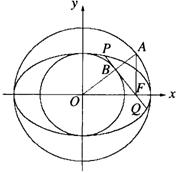
本小題主要考查橢圓的標準方程和幾何性質、直線方程、平面向量、曲線和方程的關系等解析幾何的基礎知識和基本思想方法,考查推理及運算能力.
(Ⅰ)證明:由題設條件知,Rt△OFA∽Rt△OBF,故
![]() 即
即![]() .
.
因此,c2=ab.
解:在Rt△OFA中,
FA=![]()
于是,直線OA的斜率k![]() .設直線BF的斜率為k,則
.設直線BF的斜率為k,則
k=![]()
這時,直線BF的方程為y=![]() (x-c),令x=0,則
(x-c),令x=0,則
y=![]()
所以直線BF與y軸的交點為M(0,a).

(Ⅱ)證明:由(Ⅰ),得直線BF的方程為y=kx+a,且
k2=![]() ②
②
由已知,設P(x1,y1)、Q(x2,y2),則它們的坐標滿足方程組
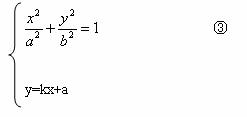
由方程組③消去y,并整理得
(b2+a2k2)x2+
由①、②和④,
x1x2=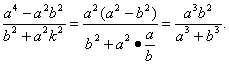
由方程組③消去x,并整理得
(b2+a2k2)y2-2ab2y+a2b2-a2b2k2=0. ⑤
由式②和⑤,
y1y2=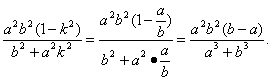
綜上,得到
![]() ·
·![]()
![]() .
.
注意到a2-ab+b2=a2-c2+b2=2b2,得
![]() ·
·![]()
![]()
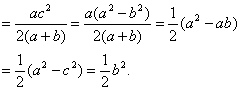


 高中必刷題系列答案
高中必刷題系列答案科目:高中數學 來源: 題型:
 已知矩形ABCD中,AB=2
已知矩形ABCD中,AB=2| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知圓O:x2+y2=2交x軸于A,B兩點,點P(-1,1)為圓O上一點.曲線C是以AB為長軸,離心率為
如圖,已知圓O:x2+y2=2交x軸于A,B兩點,點P(-1,1)為圓O上一點.曲線C是以AB為長軸,離心率為
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,F1,F2是離心率為
如圖,F1,F2是離心率為
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•日照一模)已知長方形EFCD,|EF|=2,|FC|=
(2013•日照一模)已知長方形EFCD,|EF|=2,|FC|=
| ||
| 2 |
| FA |
| FB |
| TA |
| TB |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com