
【題目】如圖,在三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為菱形,點
為菱形,點![]() 是棱
是棱![]() 上不同于
上不同于![]() ,
, ![]() 的點,平面
的點,平面![]() 與棱
與棱![]() 交于點
交于點![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求證: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求證: ![]() 平面
平面![]() ;
;
(Ⅲ)若二面角![]() 為
為![]() ,求
,求![]() 的長.
的長.

【答案】(1)詳見解析;(2)詳見解析;(3) ![]() .
.
【解析】試題分析:(Ⅰ)先利用面面平行的性質定理得到線線平行,再利用線面平行的判定定理進行求解;(Ⅱ)先利用面面垂直的性質定理和菱形的對角線相互垂直得到線線垂直,再利用線面垂直的判定定理進行證明;(Ⅲ)利用空間向量進行求解.
試題解析:(Ⅰ)因為在三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
所以![]()
![]() .
.
又因為![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)因為![]() ,所以
,所以![]() ,
,
又因為平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
所以![]()
![]() .
.
因為四邊形![]() 為菱形,所以
為菱形,所以![]()
![]() .
.
所以![]() 平面
平面![]() .
.
(Ⅲ)取線段![]() 中點
中點![]() ,因為菱形
,因為菱形![]() 中,
中, ![]() ,
,
所以![]()
![]() .
.
又因為![]()
![]()
![]() ,所以
,所以![]()
![]() .
.
又因為![]() 平面
平面![]() .
.
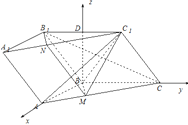
如圖,以![]() 為原點,建立空間直角坐標系
為原點,建立空間直角坐標系![]() ,
,
則![]()
![]()
所以![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
設![]() ,(
,( ![]() )
)
![]()
![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
則![]() , 即
, 即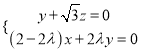 ,
,
令![]() ,則
,則![]() ,
, ![]() .
.
所以![]() .
.
由(Ⅱ)知, ![]() 是平面
是平面![]() 的一個法向量.則
的一個法向量.則
因為二面角![]() 為
為![]() ,
,
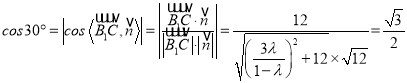 .
.
解得![]() ,或
,或![]() (舍).
(舍).
所以![]() ,即
,即![]() 的長為
的長為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】設函數![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)當![]() 時,是否存在整數
時,是否存在整數![]() ,使不等式
,使不等式![]() 恒成立?若存在,求整數
恒成立?若存在,求整數![]() 的值;若不存在,則說明理由;
的值;若不存在,則說明理由;
(3)關于![]() 的方程
的方程![]() 在
在![]() 上恰有兩個相異實根,求實數
上恰有兩個相異實根,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校游園活動有這樣一個游戲:甲箱子里裝有3個白球,2個黑球,乙箱子里裝有1個白球,2個黑球,這些球除了顏色外完全相同,每次游戲從這兩個箱子里各隨機摸出2個球,若摸出的白球不少于2個,則獲獎(每次游戲結束后將球放回原箱).
(1)求在1次游戲中:
①摸出3個白球的概率.
②獲獎的概率.
(2)求在3次游戲中獲獎次數X的分布列.(用數字作答)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的三個頂點坐標分別為A(﹣1,1),B(7,﹣1),C(﹣2,5),AB邊上的中線所在直線為l.
(1)求直線l的方程;
(2)若點A關于直線l的對稱點為D,求△BCD的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年9月,第22屆魯臺經貿洽談會在濰坊魯臺會展中心舉行,在會展期間某展銷商銷售一種商品,根據市場調查,每件商品售價x(元)與銷量t(萬元)之間的函數關系如圖所示,又知供貨價格與銷量呈反比,比例系數為20.(注:每件產品利潤=售價﹣供貨價格) 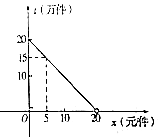
(1)求售價15元時的銷量及此時的供貨價格;
(2)當銷售價格為多少時總利潤最大,并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某鋼管生產車間生產一批鋼管,質檢員從中抽出若干根對其直徑(單位:![]() )進行測量,得出這批鋼管的直徑
)進行測量,得出這批鋼管的直徑![]() 服從正態分布
服從正態分布![]() .
.
(Ⅰ)如果鋼管的直徑![]() 滿足
滿足![]() 為合格品,求該批鋼管為合格品的概率(精確到0.01);
為合格品,求該批鋼管為合格品的概率(精確到0.01);
(Ⅱ)根據(Ⅰ)的結論,現要從40根該種鋼管中任意挑選3根,求次品數![]() 的分布列和數學期望.
的分布列和數學期望.
(參考數據:若![]() ,則
,則![]() ;
;![]() ;
;![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a>0,a≠1且loga3>loga2,若函數f(x)=logax在區間[a,2a]上的最大值與最小值之差為1.
(1)求a的值;
(2)解不等式 ![]() ;
;
(3)求函數g(x)=|logax﹣1|的單調區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com