
【題目】已知函數(shù)![]() (
(![]() ).
).
(1)設![]() 是
是![]() 的極值點,求
的極值點,求![]() ,并求
,并求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,
,![]() 在
在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減.;(2)
單調(diào)遞減.;(2)![]() .
.
【解析】
(1)由極值點的導數(shù)等于0得出![]() 的值,再由導數(shù)證明其單調(diào)性即可;
的值,再由導數(shù)證明其單調(diào)性即可;
(2)構(gòu)造函數(shù)![]() ,分類討論
,分類討論![]() 的值,利用導數(shù)得出
的值,利用導數(shù)得出![]() 的單調(diào)性,即可得出實數(shù)
的單調(diào)性,即可得出實數(shù)![]() 的取值范圍.
的取值范圍.
![]() ,由題設可知
,由題設可知![]() ,
,
即![]() ,得
,得![]() .
.
從而![]() ,則
,則![]() 單減,
單減,
且在(1,![]() )上
)上![]() >0,在(
>0,在(![]() ,+
,+![]() )上
)上![]() <0,
<0,
∴![]() 在(1,
在(1,![]() )上單增,在(
)上單增,在(![]() ,+
,+![]() )上單減,
)上單減,
又![]() ,
,![]() ,
,
∴當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() .
.
所以![]() 在
在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減.
單調(diào)遞減.
(2)設![]() ,則
,則![]() (
(![]() )
)
所以當![]() 時,
時,![]() ,知
,知![]() 在
在![]() 單調(diào)遞減
單調(diào)遞減
得![]() ,即
,即![]() 在
在![]() 也單調(diào)遞減
也單調(diào)遞減
可知![]() ,滿足題意
,滿足題意
當![]() 時,
時,![]() 在
在![]() 上成立,所以
上成立,所以![]()
即![]() 在
在![]() 上單調(diào)遞增,則
上單調(diào)遞增,則![]() ,不滿足題意
,不滿足題意
當![]() 時,
時,![]() ,所以
,所以![]()
即![]() 在
在![]() 上單調(diào)遞增,則
上單調(diào)遞增,則![]() ,不滿足題意
,不滿足題意
綜上可知:當![]() 時,
時,![]() 成立
成立


 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數(shù)學 來源: 題型:
【題目】根據(jù)養(yǎng)殖規(guī)模與以往的養(yǎng)殖經(jīng)驗,某海鮮商家的海產(chǎn)品每只質(zhì)量(克)在正常環(huán)境下服從正態(tài)分布![]() .
.
(1)隨機購買10只該商家的海產(chǎn)品,求至少買到一只質(zhì)量小于![]() 克該海產(chǎn)品的概率.
克該海產(chǎn)品的概率.
(2)2020年該商家考慮增加先進養(yǎng)殖技術投入,該商家欲預測先進養(yǎng)殖技術投入為49千元時的年收益增量.現(xiàn)用以往的先進養(yǎng)殖技術投入![]() (千元)與年收益增量
(千元)與年收益增量![]() (千元)(
(千元)(![]() )的數(shù)據(jù)繪制散點圖,由散點圖的樣本點分布,可以認為樣本點集中在曲線
)的數(shù)據(jù)繪制散點圖,由散點圖的樣本點分布,可以認為樣本點集中在曲線![]() 的附近,且
的附近,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,其中
,其中![]() ,
,![]() =
=![]()
![]() .根據(jù)所給的統(tǒng)計量,求
.根據(jù)所給的統(tǒng)計量,求![]() 關于
關于![]() 的回歸方程,并預測先進養(yǎng)殖技術投入為49千元時的年收益增量.
的回歸方程,并預測先進養(yǎng)殖技術投入為49千元時的年收益增量.
附:若隨機變量![]() ,則
,則![]() ,
,![]() ;
;
對于一組數(shù)據(jù)![]() ,
,![]() ,
,![]() ,
,![]() ,其回歸線
,其回歸線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為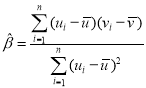 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(本小題滿分10分)選修4—4,坐標系與參數(shù)方程
已知曲線![]() ,直線
,直線![]() :
:![]() (
(![]() 為參數(shù)).
為參數(shù)).
(I)寫出曲線![]() 的參數(shù)方程,直線
的參數(shù)方程,直線![]() 的普通方程;
的普通方程;
(II)過曲線![]() 上任意一點
上任意一點![]() 作與
作與![]() 夾角為
夾角為![]() 的直線,交
的直線,交![]() 于點
于點![]() ,
,![]() 的最大值與最小值.
的最大值與最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中,以原點為極點,![]() 軸非負半軸為極軸,長度單位相同,建立極坐標系,曲線
軸非負半軸為極軸,長度單位相同,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 過點
過點![]() ,傾斜角為
,傾斜角為![]() .
.
(1)將曲線![]() 的極坐標方程化為直角坐標方程,寫出直線
的極坐標方程化為直角坐標方程,寫出直線![]() 的參數(shù)方程的標準形式;
的參數(shù)方程的標準形式;
(2)已知直線![]() 交曲線
交曲線![]() 于
于![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2019年上半年我國多個省市暴發(fā)了“非洲豬瘟”疫情,生豬大量病死,存欄量急劇下降,一時間豬肉價格暴漲,其他肉類價格也跟著大幅上揚,嚴重影響了居民的生活.為了解決這個問題,我國政府一方面鼓勵有條件的企業(yè)和散戶防控疫情,擴大生產(chǎn);另一方面積極向多個國家開放豬肉進口,擴大肉源,確保市場供給穩(wěn)定.某大型生豬生產(chǎn)企業(yè)分析當前市場形勢,決定響應政府號召,擴大生產(chǎn)決策層調(diào)閱了該企業(yè)過去生產(chǎn)相關數(shù)據(jù),就“一天中一頭豬的平均成本與生豬存欄數(shù)量之間的關系”進行研究.現(xiàn)相關數(shù)據(jù)統(tǒng)計如下表:
生豬存欄數(shù)量 | 2 | 3 | 4 | 5 | 8 |
頭豬每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 |
(1)研究員甲根據(jù)以上數(shù)據(jù)認為![]() 與
與![]() 具有線性回歸關系,請幫他求出
具有線性回歸關系,請幫他求出![]() 關于
關于![]() 的線.性回歸方程
的線.性回歸方程![]() (保留小數(shù)點后兩位有效數(shù)字)
(保留小數(shù)點后兩位有效數(shù)字)
(2)研究員乙根據(jù)以上數(shù)據(jù)得出![]() 與
與![]() 的回歸模型:
的回歸模型:![]() .為了評價兩種模型的擬合效果,請完成以下任務:
.為了評價兩種模型的擬合效果,請完成以下任務:
①完成下表(計算結(jié)果精確到0.01元)(備注:![]() 稱為相應于點
稱為相應于點![]() 的殘差);
的殘差);
生豬存欄數(shù)量 | 2 | 3 | 4 | 5 | 8 | |
頭豬每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 | |
模型甲 | 估計值 | |||||
殘差 | ||||||
模型乙 | 估計值 | 3.2 | 2.4 | 2 | 1.76 | 1.4 |
殘差 | 0 | 0 | 0 | 0.14 | 0.1 | |
②分別計算模型甲與模型乙的殘差平方和![]() 及
及![]() ,并通過比較
,并通過比較![]() 的大小,判斷哪個模型擬合效果更好.
的大小,判斷哪個模型擬合效果更好.
(3)根據(jù)市場調(diào)查,生豬存欄數(shù)量達到1萬頭時,飼養(yǎng)一頭豬每一天的平均收入為7.5元;生豬存欄數(shù)量達到1.2萬頭時,飼養(yǎng)一頭豬每一天的平均收入為7.2元若按(2)中擬合效果較好的模型計算一天中一頭豬的平均成本,問該生豬存欄數(shù)量選擇1萬頭還是1.2萬頭能獲得更多利潤?請說明理由.(利潤=收入-成本)
參考公式: .
.
參考數(shù)據(jù):![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() (
(![]() )的離心率為
)的離心率為![]() ,以
,以![]() 的短軸為直徑的圓與直線
的短軸為直徑的圓與直線![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)直線![]() 交
交![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() .已知
.已知![]() 上存在點
上存在點![]() ,使得
,使得![]() 是以
是以![]() 為頂角的等腰直角三角形,若
為頂角的等腰直角三角形,若![]() 在直線
在直線![]() 的右下方,求
的右下方,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2022年北京冬奧會的申辦成功與“3億人上冰雪”口號的提出,將冰雪這個冷項目迅速炒“熱”.北京某綜合大學計劃在一年級開設冰球課程,為了解學生對冰球運動的興趣,隨機從該校一年級學生中抽取了100人進行調(diào)查,其中女生中對冰球運動有興趣的占![]() ,而男生有10人表示對冰球運動沒有興趣額.
,而男生有10人表示對冰球運動沒有興趣額.
(1)完成![]() 列聯(lián)表,并回答能否有
列聯(lián)表,并回答能否有![]() 的把握認為“對冰球是否有興趣與性別有關”?
的把握認為“對冰球是否有興趣與性別有關”?
有興趣 | 沒興趣 | 合計 | |
男 | 55 | ||
女 | |||
合計 |
(2)已知在被調(diào)查的女生中有5名數(shù)學系的學生,其中3名對冰球有興趣,現(xiàn)在從這5名學生中隨機抽取3人,求至少有2人對冰球有興趣的概率.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系xOy下,曲線C1的參數(shù)方程為![]() (
(![]() 為參數(shù)),曲線C1在變換T:
為參數(shù)),曲線C1在變換T:![]() 的作用下變成曲線C2.
的作用下變成曲線C2.
(1)求曲線C2的普通方程;
(2)若m>1,求曲線C2與曲線C3:y=m|x|-m的公共點的個數(shù).
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com