
【題目】設圓![]() 的圓心在
的圓心在![]() 軸上,并且過
軸上,并且過![]() 兩點.
兩點.
(1)求圓![]() 的方程;
的方程;
(2)設直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,那么以
兩點,那么以![]() 為直徑的圓能否經過原點,若能,請求出直線
為直徑的圓能否經過原點,若能,請求出直線![]() 的方程;若不能,請說明理由.
的方程;若不能,請說明理由.
【答案】(1) ![]() (2)
(2) ![]() 或
或![]() .
.
【解析】試題分析:(1)圓![]() 的圓心在
的圓心在![]() 的垂直平分線上,又
的垂直平分線上,又![]() 的中點為
的中點為![]() ,
, ![]() ,∴
,∴![]() 的中垂線為
的中垂線為![]() .∵圓
.∵圓![]() 的圓心在
的圓心在![]() 軸上,∴圓
軸上,∴圓![]() 的圓心為
的圓心為![]() ,因此,圓
,因此,圓![]() 的半徑
的半徑![]() ,(2)設M,N的中點為H,假如以
,(2)設M,N的中點為H,假如以![]() 為直徑的圓能過原點,則
為直徑的圓能過原點,則![]() .
.![]() ,設
,設![]() 是直線
是直線![]() 與圓
與圓![]() 的交點,將
的交點,將![]() 代入圓
代入圓![]() 的方程得:
的方程得: ![]() .∴
.∴![]() .∴
.∴![]() 的中點為
的中點為![]() .代入即可求得
.代入即可求得![]() ,解得
,解得![]() .再檢驗即可
.再檢驗即可
試題解析:
(1)∵圓![]() 的圓心在
的圓心在![]() 的垂直平分線上,
的垂直平分線上,
又![]() 的中點為
的中點為![]() ,
, ![]() ,∴
,∴![]() 的中垂線為
的中垂線為![]() .
.
∵圓![]() 的圓心在
的圓心在![]() 軸上,∴圓
軸上,∴圓![]() 的圓心為
的圓心為![]() ,
,
因此,圓![]() 的半徑
的半徑![]() ,
,
∴圓![]() 的方程為
的方程為![]() .
.
(2)設![]() 是直線
是直線![]() 與圓
與圓![]() 的交點,
的交點,
將![]() 代入圓
代入圓![]() 的方程得:
的方程得: ![]() .
.
∴![]() .
.
∴![]() 的中點為
的中點為![]() .
.
假如以![]() 為直徑的圓能過原點,則
為直徑的圓能過原點,則![]() .
.
∵圓心![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,
∴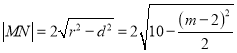 .
.
∴![]() ,解得
,解得![]() .
.
經檢驗![]() 時,直線
時,直線![]() 與圓
與圓![]() 均相交,
均相交,
∴![]() 的方程為
的方程為![]() 或
或![]() .
.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:高中數學 來源: 題型:
【題目】設復數z=2m+(4-m2)i,當實數m取何值時,復數z對應的點:
(1)位于虛軸上?
(2)位于一、三象限?
(3)位于以原點為圓心,以4為半徑的圓上?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,以
,以![]() 為圓心,橢圓的短半軸長為半徑的圓與直線
為圓心,橢圓的短半軸長為半徑的圓與直線![]() 相切.
相切.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)已知點![]() ,和面內一點
,和面內一點![]() ,過點
,過點![]() 任作直線
任作直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,設直線
兩點,設直線![]() 的斜率分別為
的斜率分別為![]() ,若
,若![]() ,試求
,試求![]() 滿足的關系式.
滿足的關系式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設有一條光線從![]() 射出,并且經
射出,并且經![]() 軸上一點
軸上一點![]() 反射.
反射.
(1)求入射光線和反射光線所在的直線方程(分別記為![]() );
);
(2)設動直線![]() ,當點
,當點![]() 到
到![]() 的距離最大時,求
的距離最大時,求![]() 所圍成的三角形的內切圓(即:圓心在三角形內,并且與三角形的三邊相切的圓)的方程.
所圍成的三角形的內切圓(即:圓心在三角形內,并且與三角形的三邊相切的圓)的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解今年某校高三畢業班想參軍的學生體重情況,將所得的數據整理后,畫出了頻率分布直方圖(如圖).已知圖中從左到右的前3個小組的頻率之比為1:2:3,其中第2小組的頻數為24.
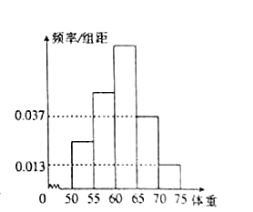
(Ⅰ)求該校高三畢業班想參軍的學生人數;
(Ⅱ)以這所學校的樣本數據來估計全省的總體數據,若從全省高三畢業班想參軍的同學中(人數很多)任選三人,設![]() 表示體重超過60公斤的學生人數,求
表示體重超過60公斤的學生人數,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() (
(![]() )與橢圓
)與橢圓![]() :
:![]() 相交所得的弦長為
相交所得的弦長為![]() .
.
(Ⅰ)求拋物線![]() 的標準方程;
的標準方程;
(Ⅱ)設![]() ,
,![]() 是
是![]() 上異于原點
上異于原點![]() 的兩個不同點,直線
的兩個不同點,直線![]() 和
和![]() 的傾斜角分別為
的傾斜角分別為![]() 和
和![]() ,當
,當![]() ,
,![]() 變化且
變化且![]() 為定值
為定值![]() (
(![]() )時,證明:直線
)時,證明:直線![]() 恒過定點,并求出該定點的坐標.
恒過定點,并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f (x)=lg(ax2+2x+1) .
(1)若函數f (x)的定義域為R,求實數a的取值范圍;
(2)若函數f (x)的值域為R,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高2010級數學培優學習小組有男生3人女生2人,這5人站成一排留影。
(1)求其中的甲乙兩人必須相鄰的站法有多少種?
(2)求其中的甲乙兩人不相鄰的站法有多少種?
(3)求甲不站最左端且乙不站最右端的站法有多少種 ?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com