
【題目】設橢圓E: ![]() +
+ ![]() =1(a>0)的焦點在x軸上.
=1(a>0)的焦點在x軸上.
(Ⅰ)若橢圓E的離心率e= ![]() a,求橢圓E的方程;
a,求橢圓E的方程;
(Ⅱ)設F1、F2分別是橢圓E的左、右焦點,P為直線x+y=2 ![]() 與橢圓E的一個公共點,直線F2P交y軸于點Q,連結F1P,問當a變化時,
與橢圓E的一個公共點,直線F2P交y軸于點Q,連結F1P,問當a變化時, ![]() 與
與 ![]() 的夾角是否為定值,若是定值,求出該定值,若不是定值,說明理由.
的夾角是否為定值,若是定值,求出該定值,若不是定值,說明理由.
【答案】解:(Ⅰ)由題知c2=a2﹣(8﹣a2)=2a2﹣8,由 ![]() 得
得
a4﹣25a2+100=0,故a2=5或20(舍),故橢圓E的方程為 ![]() ;
;
(Ⅱ)設P(x0 , y0),F1(﹣c,0),F2(c,0),則c2=2a2﹣8,
聯立 ![]() 得8x2﹣4
得8x2﹣4 ![]() x+a4=0,
x+a4=0,
即(2 ![]() ﹣a2)2 , 故
﹣a2)2 , 故 ![]() ,
, ![]() ,
,
直線PF2的方程為 ![]() ,令x=0,則
,令x=0,則 ![]() ,即點Q的坐標為(0,
,即點Q的坐標為(0, ![]() ),
),
故 ![]() ,
, ![]()
故 ![]() =
= ![]()
故 ![]() 與
與 ![]() 的夾角為定值
的夾角為定值 ![]() .
.
【解析】(Ⅰ)由題知c2=a2﹣(8﹣a2)=2a2﹣8,由 ![]() 得a4﹣25a2+100=0,可得a2;(Ⅱ)設P(x0 , y0),F1(﹣c,0),F2(c,0),則c2=2a2﹣8,聯立
得a4﹣25a2+100=0,可得a2;(Ⅱ)設P(x0 , y0),F1(﹣c,0),F2(c,0),則c2=2a2﹣8,聯立 ![]() 得點P坐標,寫出直線PF2的方程求出點Q的坐標.由
得點P坐標,寫出直線PF2的方程求出點Q的坐標.由 ![]() =
= ![]() ,可得
,可得 ![]() 與
與 ![]() 的夾角
的夾角
【考點精析】關于本題考查的橢圓的標準方程,需要了解橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() 才能得出正確答案.
才能得出正確答案.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:
【題目】若函數f(x)滿足 ![]() ,當x∈[0,1]時,f(x)=x,若在區間(﹣1,1]上,方程f(x)﹣4ax﹣a=0有兩個不等的實根,則實數a的取值范圍是 .
,當x∈[0,1]時,f(x)=x,若在區間(﹣1,1]上,方程f(x)﹣4ax﹣a=0有兩個不等的實根,則實數a的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() sin(2x+
sin(2x+ ![]() )+sin2x.
)+sin2x.
(1)求函數f(x)的最小正周期;
(2)若函數g(x)對任意x∈R,有g(x)=f(x+ ![]() ),求函數g(x)在[﹣
),求函數g(x)在[﹣ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A是拋物線y2=4x上的一點,以點A和點B(2,0)為直徑的圓C交直線x=1于M,N兩點.直線l與AB平行,且直線l交拋物線于P,Q兩點. (Ⅰ)求線段MN的長;
(Ⅱ)若 ![]() =﹣3,且直線PQ與圓C相交所得弦長與|MN|相等,求直線l的方程.
=﹣3,且直線PQ與圓C相交所得弦長與|MN|相等,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記f(n)為最接近 ![]() (n∈N*)的整數,如f(1)=1,f(2)=1,f(3)=2,f(4)=2,f(5)=2,…,若
(n∈N*)的整數,如f(1)=1,f(2)=1,f(3)=2,f(4)=2,f(5)=2,…,若 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() =4054,則正整數m的值為( )
=4054,則正整數m的值為( )
A.2016×2017
B.20172
C.2017×2018
D.2018×2019
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《孫子算經》是我國古代的數學著作,其卷下中有類似如下的問題:“今有方物一束,外周一匝有四十枚,問積幾何?”如右圖是解決該問 題的程序框圖,若設每層外周枚數為a,則輸出的結果為( )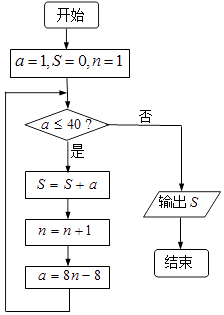
A.81
B.74
C.121
D.169
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體是由棱臺ABC﹣A1B1C1和棱錐D﹣AA1C1C拼接而成的組合體,其底面四邊形ABCD是邊長為2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2. 
(Ⅰ)求證:平面AB1C⊥平面BB1D;
(Ⅱ)求二面角A1﹣BD﹣C1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,直線l的方程是y=8,圓C的參數方程是 ![]() (φ為參數).以O為極點,x軸的非負半軸為極軸建立極坐標系.
(φ為參數).以O為極點,x軸的非負半軸為極軸建立極坐標系.
(1)求直線l和圓C的極坐標方程;
(2)射線OM:θ=α(其中 ![]() )與圓C交于O、P兩點,與直線l交于點M,射線ON:
)與圓C交于O、P兩點,與直線l交于點M,射線ON: ![]() 與圓C交于O、Q兩點,與直線l交于點N,求
與圓C交于O、Q兩點,與直線l交于點N,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個幾何體的三視圖如圖所示,則這個幾何體的表面積為( ) 
A.24+8 ![]() +8
+8 ![]()
B.20+8 ![]() +4
+4 ![]() ??
??
C.20+8 ![]() +4
+4 ![]()
D.20+4 ![]() +4
+4 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com